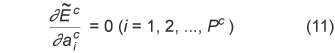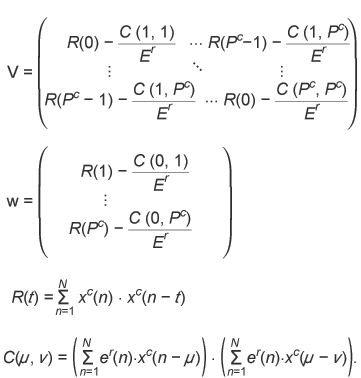|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Selected Papers: Research Activities in Laboratories of New NTT Fellows Vol. 5, No. 12, pp. 17–28, Dec. 2007. https://doi.org/10.53829/ntr200712sp2 Enhancement of MPEG-4 ALS Lossless Audio CodingAbstractEnhanced codec software that complies with the MPEG-4 Audio Lossless Coding (ALS) has been developed. To improve the compression performance, a new linear prediction analysis method for multichannel coding was devised. Moreover, to reduce the processing time, software implementation has been optimized by utilizing simplified algorithms and efficient instructions for parallel execution. The results of a comprehensive evaluation show that the new software yields a compressed file size that is 0.1% smaller on average and an encoding speed that is as much as six times higher than that of the MPEG reference software. This software will be very useful in practice because the compressed bitstream remains compliant with the international standard.
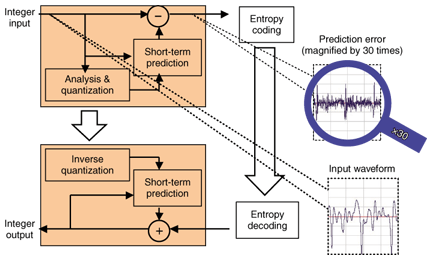
1. IntroductionThe MPEG-4 Audio Lossless Coding (ALS) standard was published in March 2006 [1], as a result of official balloting and the efforts of a number of technical contributors, including the Technical University of Berlin (Germany), RealNetworks Corp. (USA), I2R (Singapore), and NTT (Japan) [2]–[6]. This standard is intended for the compression of high-definition audio signals (high sampling rates, high word resolution, and multichannel signals) with the assurance of perfect reconstruction. It provides top-class compression performance and has some additional advantages in terms of interoperability, long-term maintenance, and clear IPR (intellectual property rights) status over other freeware or proprietary technologies. All of these merits have been gained because MPEG-4 ALS is an open international standard. Like other MPEG standards, it specifies the bitstream syntax and the decoding and reconstruction procedures; however, the encoding process has some room for future modification. In this paper, we describe our efforts to improve the compression performance and reduce the processing time within framework of the MPEG-4 ALS standard. To improve the compression performance, we have devised a new linear prediction analysis method for multichannel signals. In the conventional multichannel coding (MCC) encoder, adaptively weighted subtraction is carried out between the linear prediction residual signals of the coding channel and that of the reference channel as a result of independent linear prediction. In the new prediction analysis, the subtracted residual signal is taken into account to reduce the code length of the prediction residual signal. In other words, the coefficients of the conventional linear prediction, strictly speaking, do not minimize the subtracted residual signals that can be transmitted, whereas those of our newly devised linear prediction do minimize them. To reduce the processing time, we investigated the time-consuming components in the ALS encoder, which are the long-term prediction (LTP), MCC, and hierarchical block switching (BS) tools. The existing versions of these tools can significantly improve compression performance, but they do so at the cost of encoder complexity. In our studies, we developed simplified algorithms for LTP, MCC, BS, and other processing modules, starting from the MPEG-4 reference software. In addition, we improved the software implementation and used simultaneous single-input multiple-output execution to enhance the execution speeds of the encoder and decoder. Several freeware lossless audio codecs are available, with updated versions offered when new features are created or bugs are found. In contrast, an international standard cannot be easily amended, so it is important to make consistent improvement in compression performance, even if by only 0.1%, while maintaining compatibility with the standard. The accumulation of efforts in this area may raise the compression limit. After briefly overviewing the MPEG-4 ALS structure, we explain our methods for enhancing compression and reducing encoder complexity. Then, we present our experimental results. 2. Basic structure of MPEG-4 ALS2.1 Predictive codingMPEG-4 ALS technology is based on time-domain linear prediction. A diagram outlining the encoding and decoding processes is shown in Fig. 1. Linear prediction technology has been widely used in speech coding systems, such as those used in cellular and IP (Internet protocol) phones. A P-th order linear prediction analysis provides estimates of the prediction parameters ak(k = 1, 2, ..., P) that minimize the prediction residual e(n) between the input value x(n) and the value 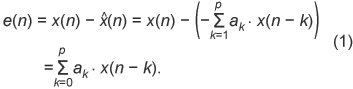
The integer value of the prediction residual signal and the quantized partial autocorrelation (PARCOR [7]) coefficients obtained from the prediction parameters are transmitted to the decoder. The decoder has a recursive filter that can reconstruct the original waveform losslessly from the transmitted bitstream. Actually, the residual signal has a smaller amplitude than the input signal does, and the amplitude can be compressed by means of entropy coding using a Golomb-Rice code or block Gilbert-Moore code [8], [9]. Obviously, the smaller the amplitude, the shorter the code length. Therefore, the minimum code length can be obtained approximately by minimizing the energy of the input signal of every frame. The PARCOR coefficients are also compressed with Rice code and are convenient for checking stability. The prediction order can be adaptively set from 0 (no prediction) to 1023. Additionally, progressive order prediction is used at the initial samples of the random access frames [10]. It should be mentioned that the analysis method for linear prediction is not a concern in the standard bitstream. The Levinson-Durbin (LD) method is implemented in the reference software, though other methods, such as the Burg method, the covariance-lattice method [11], and Laguerre-based pure linear prediction (L-PLP) [12], are acceptable for ALS. In contrast, the conventional stereo prediction methods for lossless audio coding [13]–[15] are fundamentally incompatible with those in MPEG-4 ALS in that they need cross-prediction coefficients, whose transmission is forbidden in the ALS bitstream. 2.2 LTPNormal linear prediction, especially the short-term linear prediction described above, utilizes the correlation between neighboring samples to reduce the amplitude. Speech and audio signals sometimes have long-term correlation due to the pitch. This correlation can be used to further reduce the amplitude of the residual signal and thereby reduce the bit rate. As shown in Fig. 2, multi-tap LTP is sequentially applied to the short-term prediction residual signal. To reduce the amplitude, the best delay parameter is found and a set of predictive coefficients is calculated. These are also compressed by Rice code and transmitted as side information.
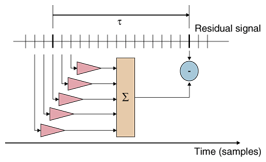
At the encoder, short-term prediction residual signal e(n) is further predicted by the following formula: At the decoder, the reverse process is carried out by means of the recursive filtering and the reconstructed residual signal e(n) is used for short-term LPC synthesis. 2.3 MCCThere is inter-channel correlation between multiple channels. Inter-channel prediction is applied to the prediction error to reduce the amplitude of the prediction residual after short-term linear prediction or long-term prediction. For multichannel coding, a search is performed to find the channel-pair combination that provides the maximum inter-channel correlation. For the selected channel-pair, multi-tap inter-channel prediction is applied. In addition, the relative delay parameter between the channel-pair is found and the associated weighting coefficients are determined. All these coefficients are then quantized and compressed by Rice code. Lossless audio coding technology will be widely used for compressing various multichannel signals, such as wave-field-synthesis, bio-medical, and seismic signals as well as surround audio signals. To improve the compression performance for these multichannel signals, adaptive subtraction from reference channels with weighting factors is applied. This process is based on the inter-channel dependence of the time domain prediction residual signal. There are three modes for each channel and each frame: an independent coding mode, a second mode with three taps, and a third one with six taps (i.e., three delayed taps in addition to the three in the second mode), as shown in Fig. 3. At least one channel must be encoded in the independent coding mode for lossless decoding of all the channels.
For the three-tap mode, the operation is performed as follows. where The reconstructed residual signal ec(n) is used for short-term LPC synthesis or LTP decoding. For the six-tap mode, adaptive subtraction is carried out using 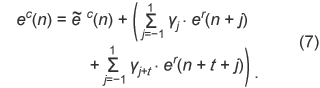
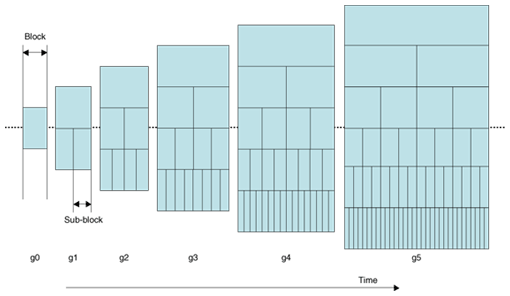
Again, the reconstructed residual signal ec(n) is used for short-term LPC synthesis or LTP decoding. 2.4 Hierarchical BSThe ALS standard has a hierarchical block-switching scheme that further enhances compression performance, as shown in Fig. 4. The encoder can select the best combination of sub-blocks in a frame. Mode g1 can adaptively select two sub-block lengths for every block, while mode g0 can use only one block length. The number of sub-blocks can be 32 in the case of mode g5. A longer block length tends to be useful for stationary signals, while a shorter block length is effective for non-stationary signals.
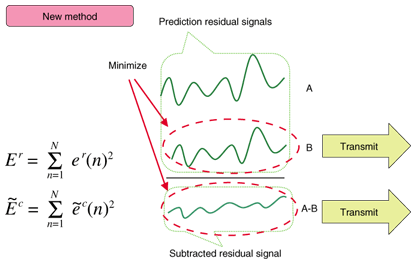
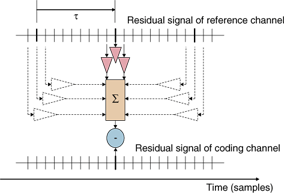
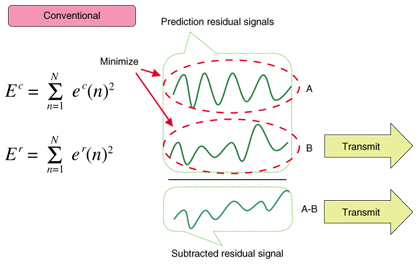
2.5 Other featuresFor a floating-point signal, MPEG-4 ALS has a compression tool that makes use of the fundamental compression structure of an integer signal [16], [17]. The floating-point format is useful for professional mixing of music because there is no risk of overflow or underflow. However, this format cannot be compressed because its nominal value has no correlation between samples. We have therefore invented a novel scheme that decomposes a floating-point signal sequence into integer and remaining sequences. We have also introduced the approximate common factor scheme, which greatly improves the compression performance when an input floating-point value sequence is generated from the integer value sequence multiplied by a common number throughout the frame. The common number can be detected by means of rational approximations even though the input samples have errors due to truncation or some other operations. The remaining sequence is further compressed by masked Lempel-Ziv compression, making full use of the properties inherited from the decomposition processes. There are a number of other control parameters for the encoder, and it should be possible to efficiently estimate them in the future without losing conformity to the standard [18], [19]. 3. Enhancement of MPEG-4 ALS3.1 Linear prediction tool for MCCIn conventional linear prediction analysis methods, as shown in Fig. 5, the prediction parameters are estimated to minimize the prediction residuals of each channel independently. Therefore, the prediction parameters of the reference channel
However, in the coding channel, we should minimize the energy of the subtracted signal 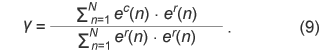
From Eqs. (6) and (7), 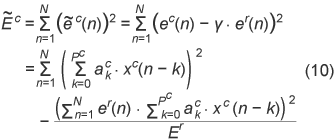
Then, to minimize Eq. (10), we derive the prediction parameters Equation (12) can be solved by the Cholesky decomposition method because matrix V is not a Toeplitz matrix but a symmetric one. Sometimes a synthesis filter with these prediction parameters may be unstable. In such a case, the usual Levinson-Durbin method can be used to minimize Ec instead of our new method. In addition, the bitstreams derived from the conventional method and from our new method are compared and the smaller one is transmitted. This guarantees that the best possible compression performance is always obtained.
3.2 Complexity reduction3.2.1 Calculating auto-correlation coefficientsAuto-correlation coefficients are essential for short-term linear prediction analysis. The computational cost becomes greater as the prediction order and/or the number of samples per frame increases. To reduce the computational complexity, fast Fourier transformation (FFT) is used when the prediction order is large. Similarly, the most time-consuming operation in the LTP encoder is the auto-correlation calculation for determining delay parameter τ. For sampling rates of 192 kHz or higher, delay parameter values can range from the maximum short-term prediction order to that plus 1024. Under these conditions, FFT can significantly reduce the processing time for calculating auto-correlation coefficients. 3.2.2 Simplified algorithm for MCCMCC encoding and decoding processes are flexibly defined for signals with various numbers of channels up to 65,536. Selecting the reference channel generally requires a computational load. For music applications, two-channel stereo signals are the most important. As far as stereo input is concerned, the procedure for selecting the reference channel can be greatly reduced by simply comparing the energy of the two signals. In addition, only a three-tap filter can be used for stereo signals, although a six-tap filter is effective for multichannel signals recorded using a linear array of microphones. 3.2.3 Simplified hierarchical BSTo find the best sub-block division, we need to calculate the actual code length for all sub-block combinations exhaustively. The total processing time is roughly proportional to the number of layers in the hierarchy. We can reduce the complexity by means of a sub-optimal search using the estimated code length and by reusing the intermediate calculation results among layers. 4. Experimental evaluation4.1 ConditionsTo evaluate our methods, we performed encoding and decoding experiments for musical signals. As input signals, we used 13 copyright-free music items of CD (compact disc) quality (stereo, sampling rate: 44.1 kHz, word length: 16 bits, duration: 64 minutes, file size: 642 MB) composed by one of the authors (Y.K.) and 20 CD songs with English lyrics from the RWC music database (RWC-MDB-P-2001 No. 81–100, 85 min., 855 MB) [20]. These are similar to copyright popular songs. The obtained encoding or decoding times are the total processing times for all input signals (the faster the better) measured in seconds using “timeit.exe” on a Microsoft Windows Server 2003 with an AMD Opteron processor operating at 2.4 GHz with 2 GB of memory and normalized by the duration time (the smaller the faster; 50% means double speed). We defined the compression ratio (the smaller the better) in percent as 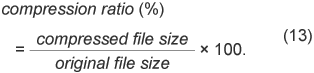
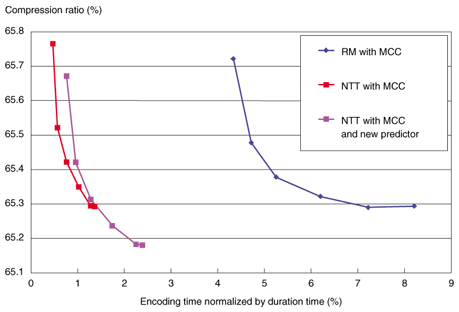
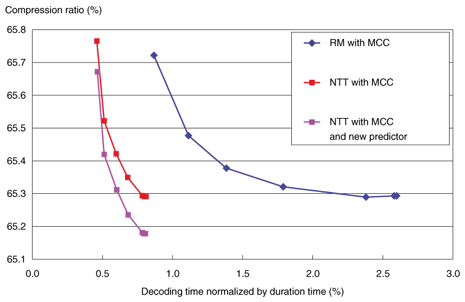
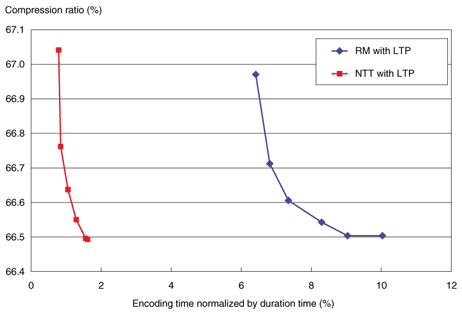
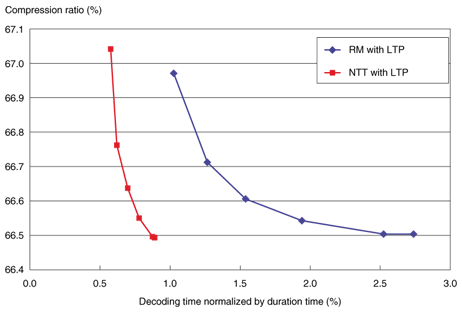
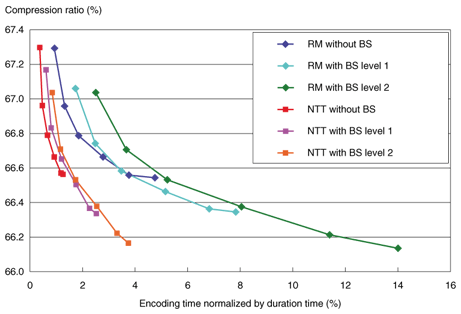
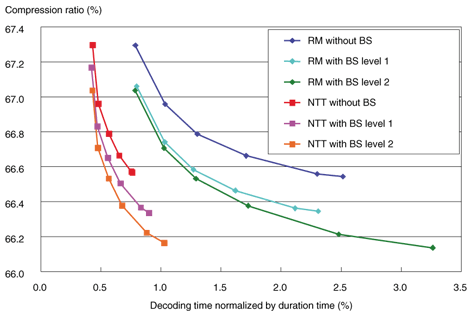
4.2 ResultsThe experimental results are shown in Figs. 7–12, where the six symbols on each curve correspond to systems with different maximum prediction orders of 7, 15, 31, 63, 127, and 255, from top to bottom. The encoding time and compression ratio with MCC are also shown in Fig. 7. Our software (red line: NTT with MCC) reduced the encoding time to 1/6 compared with the reference software (blue line: RM with MCC). Furthermore, our linear prediction tool for MCC (purple line: NTT with MCC and new predictor) yielded 0.1% better compression than the conventional MCC. At the decoder, as shown in Fig. 8, the decoding time was reduced to 1/2 of the reference model (blue line: RM with MCC) as a result of the efficient software implementation (red line: NTT with MCC). And the new prediction tool (purple line: NTT with MCC and new predictor) offered better compression performance than the conventional one (red line) with no increase in decoding time. In other words, the bitstream compressed by the developed method can be decoded faster than the one compressed by the conventional method with higher prediction order, yielding the same compression performance. Encoding times for LTP are compared in Fig. 9. The encoding time could be reduced to 1/5 of the reference model (blue line: RM with LTP) by the simplified encoder (red line: NTT with LTP). The decoding time and compression ratio with LTP are shown in Fig. 10. The decoding time was reduced to 1/2 that of the reference model (blue line: RM with LTP) because of the optimized implementation (red line: NTT with LTP). The BS encoding time and compression ratio are shown in Fig. 11. Our software (purple and orange lines: NTT with BS levels 1 and 2) reduced the encoding time to 1/3 compared to the reference model (light blue and green lines: RM with BS levels 1 and 2). The difference in processing speed became larger as the block switching level increased. Decoding times for BS are shown in Fig. 12. We can see that the software improved by NTT (red, purple, and orange lines: NTT) could reduce the decoding time by 1/3, compared with the reference model (blue, light blue, and green lines: RM). In summary, the software enhanced by NTT can generate a smaller bitstream, while remaining compliant to MPEG-4 ALS. As shown in Figs. 7–12, the processing time of this enhanced software (NTT proprietary) is shorter than that of the reference model software (RM) overall.
5. ConclusionWe have developed enhanced codec software that complies with the MPEG-4 Audio Lossless Coding (ALS). A comprehensive evaluation showed that it yields a slightly smaller (0.1%) compressed file size on average and an encoding speed that is as much as six times higher than that of the MPEG reference software. For the decoder, efficient software implementation reduced the processing time by half. This software is very practical because the compressed bitstream remains compliant with the international standard. This standard is expected to provide common tools for various applications [21] and should continue to be maintained so that the compressed files can be perfectly decoded even 100 years from now. Potential applications include audio signal archiving, professional audio editing, portable music players, and editing or archiving time series signals other than audio ones, such as medical or environmental data. References
|
|||||||||||||||||||||||||||||||||||||||||||||







 = 1):
= 1):