New Paradigm for Practical Cryptosystems without Random Oracles

2.1 Notation

is the set of natural numbers and is the set of real numbers. ⊥ denotes a null string.

A function f : →−is negligible in k, if for every constant c > 0, there exists integer n such that f(k) < k^−c for all k > n.

If A is a probabilistic machine or algorithm, A(x) denotes the random variable of A's output on input x. Then, yR← A(x) denotes that y is randomly selected from A(x) according to its distribution. If a is a value, A(x) → a denotes the event that A outputs a on input x. If A is a set, y U← A denotes that y is uniformly selected from A. If A is a value, y ← A denotes that y is set to A.

In this paper, the underlying machines are considered to be uniform Turing machines, but the results can easily be extended to non-uniform Turing machines.

2.2 Decisional Diffie-Hellman (DDH) assumption

Let k be a security parameter and be a group with security parameter k, where the order of is prime p and |p| = k. Let {}_k be the set of groups with security parameter k.

For all k∈, we define the sets and as follows:

(k)←{(, G₁, G₂, G^x₁, G^x₂) | U← {}_k, (G₁, G₂) U← ², x U← _p}

(k)←{(, G₁, G₂, y₁,y₂) | U← {}_k, (G₁, G₂, y₁, y₂) U← ⁴}.

Let A be a probabilistic polynomial-time machine. For all k ∈, we define the DDH advantage of A as

AdvDDHA(k) ← | Pr [A(1^k, ρ)→1| ρ U← (k)] − Pr [A(1^k, ρ) → 1|ρ U← (k)] |.

The DDH assumption for {}_k∈ is: For any probabilistic polynomial-time adversary A, AdvDDHA(k) is negligible in k.

2.3 Pseudo-random Function (PRF)

Let k∈ be a security parameter. A PRF family F associated with {Seed_k}_k∈, {Dom_k}_k∈ and {Rng_k}_k∈ specifies two items:

– A family of random seeds {Seek_k}_k∈.

– A family of PRFs indexed by k,Σ R← Seed_k, σ U← Σ, D R← Dom_k, and R R← Rng_k, where each such function F^k_σ^,Σ,D,R maps an element of D to an element of R. There must exist a deterministic polynomial-time algorithm that on input 1^k,σ, and ρ, outputs F^k_σ^,Σ,D,R (ρ).

Let A^O be a probabilistic polynomial-time machine with oracle access to O. For all k, we define AdvPRFF, A(k) ←|Pr [A^F(1^k,D,R )→1] − Pr[A^RF(1^k,D,R ) → 1]|, where Σ R← Seed_k, σ U← Σ, D R← Dom_k, R R← Rng_k, F ←F^k_σ^,Σ,D,R, and RF : D → R is a truly random function (∀ρ∈D RF(ρ) U←R).

F is a PRF family if, for any probabilistic polynomial-time adversary A, AdvPRFF, A(k) is negligible in k.

2.4 Pseudo-random function with pairwise-independent random sources (πPRF)

Here, we introduce a specific class of PRFs, πPRFs.

Let k∈ be a security parameter and F be a PRF family associated with {Seed_k}_k∈, {Dom_k}_k∈, and {Rng_k}_k∈.

We then define a πPRF family for F.

Let Σ R← Seed_k, D R← Dom_k, R R← Rng_k, and RF: D → R be a truly random function (∀ρ∈DRF(ρ) U← R).

Let I_Σ be a set of indices regarding Σ such that there exists a deterministic polynomial-time algorithm, f_Σ: I_Σ → Σ, that on input i ∈_IΣ, outputs σ_i ∈Σ .

Let σ_i0, σ_i1, ..., σ_it(k) be random variables indexed by I_Σ, where i_j ∈I_Σ (j = 0, 1, ..., t(k)) and t(k) is a polynomial of k. Let σ_i0 be pairwisely independent from other variables, σ_i1, ..., σ_it(k) and each variable be uniformly distributed over Σ. That is, for any pair of (σ_i0, σ_ij) (j = 1, ..., t(k)), for any (x, y)∈Σ², Pr[σ_i0→ x ∧σ_ij → y] = Pr[σ_i0 → x ] • Pr[σ_ij → y] = 1/|Σ|².

Let A^{F, IΣ} be a probabilistic polynomial-time machine A that queries q_j ∈D along with i_j ∈I_Σ to F and receives the reply F ^k_σij^,Σ,D,R (q_j) for each j = 0, 1, ..., t(k).

Let A^{RF, IΣ} be the same as A^{F, IΣ} except that Fk_σij^{k, Σ D, R,} (q₀) is replaced by RF(q₀).

For all k, we define

AdvπPRFF, IΣ, A(k) ← |Pr[A^{F, IΣ}(1k,D ,R ) → 1] − Pr[A^{RF, IΣ}(1^k,D ,R ) → 1]|.

F is a πPRF family with index {(I_Σ, f_Σ)}_{Σ∈Seedk, k∈} if for any probabilistic polynomial-time adversary A,AdvπPRFF, IΣ, A (k) is negligible in k.

2.5 Target collision resistant (TCR) hash function

Let k∈ be a security parameter. A TCR hash function family H associated with {Dom_k}_k∈ and {Rng_k}_k∈ specifies two items:

– A family of key spaces indexed by k. Each such key space is a probability space of bit strings denoted by KH_k. There must exist a probabilistic polynomial-time algorithm whose output distribution on input 1^k is equal to KH_k.

– A family of hash functions indexed by k, h R← KH_k, D R← Dom_k, and R R← Rng_k, where each such function H_h^k,D,R maps an element of D to an element of R. There must exist a deterministic polynomial-time algorithm that on input 1^k, h, and ρ, outputs H_h^k,D,R (ρ).

Let A be a probabilistic polynomial-time machine. For all k, we define AdvTCR H, A(k)← Pr [ρ∈D ∧ρ≠ρ^* ∧H_h^k,D,R (ρ) =H_h^k,D,R (ρ^*)ρ| R← A(1^k, ρ^*, h, D, R)], where D R← Dom_k, R R← Rng_k, ρ^* U← D and h R← KH_k. H is a TCR hash function family if for any probabilistic polynomial-time adversary A, AdvTCR H, A(k) is negligible in k.

2.6 PKI-based authenticated key exchange (AKE) and eCK security definition

This section outlines the eCK security definition [16] for two-pass AKE protocols based on the public key infrastructure (PKI) model and follows the description in [17].

The eCK definition assumes that there are n parties, which are modeled as probabilistic polynomial-time Turing machines. We assume that these parties have agreed some common parameters (common reference strings) in the AKE protocol before the protocol is started. The parameter selection mechanism is out of the scope of the AKE protocol and the (eCK) security model.

Each party has a static public-private key pair together with a certificate that binds the public key to that party. ˆA (or ˆB ) denotes the static public key A (or B) of party A(B) together with a certificate. The certifying authority (CA) is not assumed to require parties to prove possession of their static private keys, but the CA is required to verify that the static public key of a party belongs to the domain of public keys.

Here, two parties exchange static public keys A, B and ephemeral public keys X, Y; the session key is obtained by combining A, B, X, Y and possibly session identities. A party A can be activated to execute an instance of the protocol called a session. Activation is made via an incoming message that has one of the following forms: ( ˆA, ˆB) or ˆB, ˆA, X). If A was activated with ( ˆA, ˆB), then A is called the session initiator; otherwise, it is called the session responder. Session initiator A creates ephemeral public-private key pair (X, x) and sends ( ˆB, ˆA, X) to session responder B. B then creates ephemeral public-private key pair (Y, y) and sends ( ˆA, ˆB, X, Y) to A.

The session of initiator A with responder B is identified via session identifier ( ˆA, ˆB, X, Y), where A and B are said to be the owner and peer of the session, respectively. The session of responder B with initiator A is identified as ( ˆB, ˆA, Y, X), where B is the owner and A is the peer. Session ( ˆB, ˆA, Y, X) is said to be a matching session of ( ˆA, ˆB, X, Y). We say that a session is completed if its owner computes a session key.

The adversary M is modeled as a probabilistic polynomial-time Turing machine and controls all communications. Parties submit outgoing messages to the adversary, who makes decisions about their delivery. The adversary presents parties with incoming messages via Send(message), thereby controlling the activation of sessions. In order to capture private information that may leak, adversary M is allowed the following queries:

– EphemeralKeyReveal(sid) The adversary obtains the ephemeral private key associated with session sid.

– SessionKeyReveal(sid) The adversary obtains the session key for session sid, provided that the session has a session key.

– StaticKeyReveal(pid) The adversary learns the static private key of party pid.

– EstabllishPatry(pid) This query makes it possible for the adversary to register a static public key on behalf of a party. In this way, the adversary completely controls that party.

If a party pid is established by EstabllishPatry(pid) query issued by adversary M, then we call the party dishonest. If a party is not dishonest, we call it honest.

The aim of adversary M is to distinguish a session key from a random key. Formally, the adversary is allowed to make a special query Test(sid^*), where sid^* is called the target session. The adversary is then given with equal probability either the session key K^*, held by sid^*, or a random key R^* U← {0, 1}^|K*|. The adversary wins the game if he correctly guesses whether the key is random or not. To define the game, we need the notion of a fresh session as follows:

Definition 1. (fresh session) Let sid be the session identifier of a completed session owned by an honest party A with peer B, who is also honest. Let —sid be the session identifier of the matching session of sid, if it exists. We define session sid to be fresh if none of the following conditions hold:

–M issues a SessionKeyReveal(sid) query or a SessionKeyReveal(—sid) query (if —sid exists),

– —sid exists and M makes either of the following queries:

both StaticKeyReveal(A) and EphemeralKeyReveal(sid) or

both StaticKeyReveal(B) and EphemeralKeyReveal(—sid),

– —sid does not exist and M makes either of the following queries:

both StaticKeyReveal(A) and EphemeralKeyReveal(sid) or StaticKeyReveal(B).

Now we are ready to present the eCK security notion.

Definition 2. (eCK security) Let K^* be the session key of the target session sid^* that should be fresh, R^* U← {0, 1}^|K*|, and b^* U← {0, 1}. As a reply to Test(sid^*) query by M, K^* is given to M if b^* = 0; R^*; otherwise, R^* is given. Finally, M outputs b ∈{0, 1}. We define
AdvAKEM(k) ← |Pr[b = b^*] − 1/2|.

A key exchange protocol is secure if the following conditions hold:

– If two honest parties complete matching sessions, then they both compute the same session key (or both output an indication of protocol failure).

– For any probabilistic polynomial-time adversary M, AdvAKEM(k) is negligible in k.

This security definition is stronger than the original form of Canetti-Krawczyk security [11] and it simultaneously captures all the known desirable security properties for authenticated key exchange including resistance to key-compromise impersonation attacks, weak perfect forward secrecy, and resilience to the leakage of ephemeral private keys.

2.7 Key encapsulation mechanism (KEM)

A KEM scheme is the triplet of algorithms, Σ= (K, E, D), where

1. K, the key generation algorithm, is a probabilistic polynomial-time algorithm that takes a security parameter k∈ (provided in unary) and returns a pair (pk, sk) of matching public and secret keys.

2. E, the key encryption algorithm, is a probabilistic polynomial-time algorithm that takes as input public key pk and outputs a key/ciphertext pair (K^*, C^*).

3. D, the decryption algorithm, is a deterministic polynomial time algorithm that takes as input secret key sk and ciphertext C^* and outputs key K^* or ⊥ (⊥ means that the ciphertext is invalid).

For all (pk, sk) output by key generation algorithm K and for all (K^*, C^*) output by key encryption algorithm E(pk), D(sk, C^*) = K^* holds. Here, the length of the key |K^*| is specified by l (k), where k is the security parameter.

Let A be an adversary. The attack game is defined in terms of an interactive computation between adversary A and its challenger C. The challenger C responds to the oracle queries made by A. The attack game (IND-CCA2 game) used to define security against adaptive chosen ciphertext attacks (IND-CCA2) is described below.

1. The challenger C generates a pair of keys (pk, sk) R← K(1^k) and gives pk to adversary A.

2. Repeat the following procedure q₁(k) times, for i = 1, . . . , q₁(k), where q₁(•) is a polynomial. A submits string C_i to a decryption oracle, DO (in C), and DO returns D_sk (C_i) to A.

3. A submits the encryption query to C. The encryption oracle EO in C selects b^* U← {0, 1} and computes (C^*, K^*) ← E(pk) and returns (C^*, K^*) to A if b^* = 0 and (C^*, K^*) if b^* = 1, where R^* U←{0, 1}^|K*| (C^* is called the target ciphertext).

4. Repeat the following procedure q₂(k) times, for j = q₁(k)+1, . . . , q₁(k) + q₂(k), where q₂(•) is a polynomial. A submits string C_j to a decryption oracle, DO (in C), subject only to the restriction that a submitted text C_j is not identical to C^*. DO returns D_sk (C_j) to A.

5. A outputs b ∈{0, 1}.

We define the IND-CCA2 advantage of A, AdvKEM_A^IND-CCA2(k) ← |Pr[b = b^*] − 1/2| in the above attack game.

We say that a KEM scheme is IND-CCA2-secure (secure against adaptive chosen ciphertext attacks) if, for any probabilistic polynomial-time adversaryA, AdvKEM_A^IND-CCA2(k) is negligible in k.

3.1 Protocol

Let k∈ be a security parameter, let U←{}_k be a group with security parameter k, and let (G₁, G₂) U← ², where the order of is prime p and |p| = k. Let H be a TCR hash function family, ˆF and ˜F be PRF families and F be a πPRF family.

(, G₁, G₂), H, F, ˜F, and ˆF are the system parameters common among all users of this AKE protocol (although ˜F and ˆF can be set privately by each party). We assume that the system parameters are selected by a trusted third party.

Party A's static private key is (a₁, a₂, a₃, a₄) U← (p)⁵ and A's static public key is A₁ ← G₁^a₁ G₂^a₂, A₂ ← G₁^a₃ G₂^a₄. Here, h_A R← KH_k indexes a TCR hash function H_A← H_hA^k,D_H,R_H, where D_H ← Π_k × ⁴, R_H ← _p, and Π_k denotes the space of possible certificates for static public keys.

Similarly, Party B's static private key is (b₀, b₁, b₂, b₃, b₄) U← (_p)⁵ and B's static public key is B₁ ← G₁^b₁ G₂^b₂, B₂ ← G₁^b₃ G₂^b₄. Here, h_B R← KH_k indexes a TCR hash function H_B ← H_hB^{k, D_H, R_H}.

A and B set πPRF and PRFs F ← F^{k,Σ_F,D_F,R_F}, ˜F ← ˜F^{k, Σ_˜F, D_˜F, R_˜F} and ˆF ← ˆF^{k,Σ _ˆF,D_ˆF,R_ˆF}, where Σ_F←, D_F← (Π_k)² × ¹⁰, R_F← {0, 1}^k, Σ_˜F ← _p, D_˜F ← {0, 1}^k, R_˜F ←(_p)², Σ_ˆF ← {0, 1}^k, D_ˆF ← {0, 1}^k, and R_ˆF ← (_p)².

To establish a session key with party B, party A performs the following procedure.

1. Select an ephemeral private key (˜x₁, ˜x₂) U← {0, 1}^k × {0, 1}^k.

2. Compute ˜a ←Σ⁴_i=0 a_i mod p (x, x₃) ← ˆF_˜x1 (1^k) + ˜F_˜a (˜x₂) mod p (as two-dimensional vectors) and the ephemeral public key (X₁ ← G^x₁, X₂ ← G^x₂, X₃ ← G₁^x₃). Note that the value of (x, x₃) (and ˜a) is only computed in a computation process of the ephemeral public key from ephemeral and static private keys.

3. Erase (x, x₃) and the whole computation history of the ephemeral public key.

4. Send ( ˆB, ˆA, X₁, X₂, X₃) to B.

Upon receiving ( ˆB, ˆA, X₁, X₂, X₃), party B verifies that (X₁, X₂, X₃) ∈³. If so, perform the following procedure.

1. Select an ephemeral private key (˜y₁, ˜y₂) U←{0, 1}^k × {0, 1}^k.

2. Compute ˜b ← Σ⁴_i=0 b_i mod p (y, y₃) ← ˆF_˜y1 (1^k) + ˜F_˜b (˜y₂) mod p (as two-dimensional vectors) and the ephemeral public key (Y₁ ← G^y₁, Y₂ ← G^y₂, Y₃ ← G₁^y3)

3. Erase (y, y₃) and the whole computation history of the ephemeral public key.

4. Send ( ˆA, ˆB, X₁, X₂, X₃, Y₁, Y₂, Y₃) to A.

Upon receiving( ˆA, ˆB, X₁, X₂, X₃, Y₁, Y₂, Y₃), party A checks if he sent ( ˆB, ˆA,X₁, X₂, X₃) to B. If so, A verifies that (Y₁, Y₂, Y₃) ∈ ³.

To compute the session key, A computes σ_A ← Y₁^a₁+ca₃Y₂^a₂+ca₄Y₃^x₃B₁^xB₂^dx , and B computes σ_B ← X₁^b₁+db₃ X₂^b₂+db₄X_3y3A₁^yA₂^cy , where c ← H_A( ˆA, ˆB,Y₁, Y₂, Y₃) and d ← H_B( ˆB, ˆA, X₁, X₂, X₃).

If they are correctly computed, then σ← σ_A (=σ_B). The session key is K ← Fσ (sid), where sid ← ( ˆA, ˆB, X₁, X₂, X₃, Y₁, Y₂, Y₃).

3.2 Security

Theorem 1.
The new AKE protocol is secure (in the sense of Definition 2) if the DDH assumption holds for {} _k∈, where H is a TCR hash function family, ˜F and ˆF are PRF families and F is a πPRF family with index {(I, f)} _∈{}k, k∈N, where I ← {(V, W, d)|(V, W, d) ∈² × _p} and f: (V, W, d) |→ V^r₁+dr₂W with (r₁, r₂) U← _p².

4.1 Scheme

This section shows a CCA-secure KEM scheme. Let k∈ be a security parameter and let U←{}_k be a group with security parameter k, where the order of is prime p and |p| = k. Let H be a TCR hash function family and F be a PRF family.

Secret key: The secret key is sk←(x₁, x₂, y₁, y₂) U← _p⁴.

Public key: G₁ U←,G₂ U←, z ← G₁^x₁ G₂^x₂ , w ← G₁^y₁ G₂^y₂, H ←H_h^k,D_H,R_H and F ← F^{k,Σ_F,D_F,R_F}, where h R← KH_k, D_H ← {pk} × ² (pk is a possible public-key value), R_H ←_p, Σ_F←, D_F← {pk} × ² and R_F← {0, 1}^k.

The public key is pk ← (, G₁, G₂, z, w, H, F).

Encryption: Choose r U← _p and compute
C₁ ← G^r₁,
C₂ ← G^r₂,
d ← H (z, w, C₁, C₂)
σ ← z^rw^rd
K ← Fσ(pk, C₁, C₂).

(C₁, C₂) is a ciphertext and K is the secret key to be shared.

Decryption: Given (z, w, C₁, C₂), check whether

(z, w, C₁, C₂)∈⁴.

If it holds, compute
d ← H (z, w, C₁, C₂)
σ ← C₁^x₁+dy₁ C₂^x₂+dy₂

K ← Fσ (pk, C₁, C₂).

4.2 CCA security

Theorem 2.

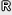
The new KEM scheme is IND-CCA2-secure if the DDH assumption holds for {}_k∈, if H is a TCR hash function family, and if F is a πPRF family with index {(I, f)}_{∈{}k, k∈} , where I ← {(V, W, d)|(V, W, d) ∈² × _p} and f : (V, W, d) |→ V^r₁+dr₂W with (r₁, r₂) U← _p².