Word-Action Mapping in Sentential Contexts By 18-Month-Old Japanese Infants
T. Kobayashi, R. Mugitani, and S. Amano
International Conference on Infant Studies, ISIS, Vol. 16, No. 1, pp. 266–267, Vancouver, 2008.
These findings demonstrate that 18-month-olds can rapidly map novel words in sentential contexts onto actions. Although previous studies found that 14-month-olds can map isolated words onto actions (Kobayashi et al., 2006), the present findings show that 14-month-olds fail to map words in sentential contexts onto actions. This suggests that a more efficient ability to extract words from ongoing fluent speech and then map them onto actions might emerge around 18 months of age.
Gender Influence on Speech Sound Processing and Word-Learning of Pitch Accent
R. Mugitani
International Conference on Infant Studies, ISIS, Vol. 16, No. 1, p. 338, Vancouver, 2008.
We found a distinct gender effect in Japanese accent discrimination and word-learning tasks. Only boys were successful in the discrimination task whereas only girls were successful in the word-learning task. Interestingly, the word-learning task even made it easier for the girls to perceive the different accent patterns, which they failed to do in a simple discrimination task. Such advantageous word learning confined to girls might lead to a gender difference in vocabulary acquisition in early language development. Future experiments with phonetically varied stimuli and different age groups will help to untangle the origin and the mechanism of the gender difference in early language development.
Diamond FETs on boron-implanted and high-pressure and high-temperature annealed homoepitaxial diamond
K. Ueda, Y. Yamauchi, and M. Kasu
Physica Status Solidi (c), Wiley VCH Verlag, Vol. 5, No. 9, pp. 3175–3177, 2008.
By combining ion-implantation and high-pressure and high-temperature (HPHT) annealing, we have obtained boron (B)-implanted diamond layers with a high hole concentration and mobility and succeeded in fabricating diamond FETs using the B-implanted layers. For a B dose of 3 × 1015 cm−2, a sheet hole concentration and mobility of 1.6 × 1013 cm−2 and 41 cm2/Vs, respectively, at 300 K were obtained. Diamond FETs fabricated on the B-implanted layer showed maximum drain current of 0.15 mA/mm at gate voltage of −2 V and maximum breakdown voltage of 530 V, corresponding to ∼1.1 MV/cm. The breakdown voltage value is comparable to those of Schottky diodes using B-doped CVD diamond films. These results confirm the high quality of the B-implanted and HPHT-annealed layers.
Stack Queue Mixed Layout of Graph Subdivisions
M. Miyauchi and G. Nakamura
Workshop on Algorithms and Computation, Kyushu Univ., Vol. 1, No. 1, pp. 145–149, 2008.
This paper studies the problem of stack queue mixed layouts of bipartite graph subdivisions. Here, an s-stack q-queue mixed layout of a graph G is defined so that each edge of G is assigned to a stack or to a queue with respect to a common vertex ordering. Recently, Dujmovic´ and Wood showed that for all integers s, q > 0, every graph G has an s-stack q-queue mixed subdivision with 
4log(s+q)q sn(G)
(resp. 2+4 log(s+q)q qn(G)) division vertices per edge, where sn(G) (resp. qn(G)) is the stack number (resp. queue number) of G. This paper deals with bipartite graphs Gm, n (m ≥ n) with m and n partite sets and shows that for all integers s, q > 0, every bipartite graph Gm, n (m ≥ n) has an s-stack q-queue mixed subdivision with 2 log(s+q)q n –1 division vertices per edge.
The Nearest Polynomial with a Zero in a Given Domain from a Geometrical Viewpoint
H. Sekigawa
ISSAC2008, ACM, Vol. 1, No. 1, pp. 287–294, Hagenberg, Austria, 2008.
For a real univariate polynomial f and a closed complex domain D, whose boundary C is a simple curve parameterized by a univariate piecewise rational function, a rigorous method is given for finding a real univariate polynomial f˜ such that f˜ has a zero in D and || f – f˜ || ∞ is minimal. First, it is proved that the minimum distance between f and polynomials having a zero at α ∈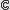 
is a piecewise rational function of the real and imaginary parts of α. Thus, on C, the minimum distance is a piecewise rational function of a parameter obtained through the parameterization of C. Therefore, by using the property that f˜ has a zero on C and computing the minimum distance on C, f˜ can be constructed.
