Quantum Communication Using Entangled Photon Pairs––Toward Quantum Repeaters

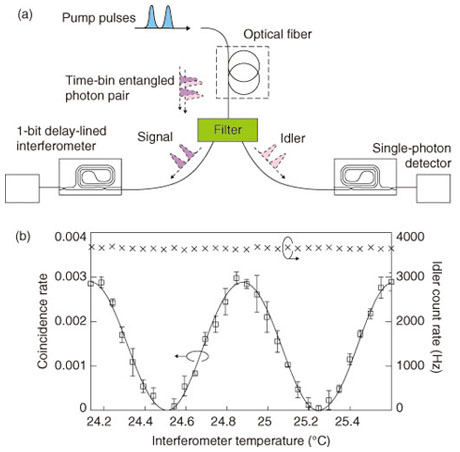
1. Introduction

In the quantum key distribution (QKD) system, whose security is based on the fact that one cannot copy a photon with an arbitrary quantum state, the key distribution distance is limited by the photon loss that occurs in the transmission medium (usually, optical fiber). In conventional optical communication systems, the transmission distance can be extended by using optical amplifiers; however, with QKD, optical amplification cannot be used to extend the distance. Therefore, the maximum key distribution distance over optical fiber in previous QKD experiments was limited to 200 km. Even if single-photon detectors are significantly improved, it is considered extremely difficult to achieve key distribution over more than 500 km of fiber. However, the distance can be increased by using entangled photon pairs. Moreover, entangled photon pairs are essential resources for building scalable quantum communication systems based on quantum repeaters.

2. Entangled photon pair generation in the telecommunication band

An entangled photon pair is a state in which two photons show a correlation that cannot be explained by classical theory [1]. For example, a polarization-entangled photon pair is a state in which the polarization state of each photon is not fixed, but the relationship between the polarization states of the two photons is predetermined. My colleagues and I have been studying time-bin entangled photon pairs, which are suitable for fiber transmission.

As the first step towards generating time-bin entangled photon pairs, we generate temporally correlated photon pairs by using spontaneous parametric processes. We input a pump light into a nonlinear medium with the 2nd- or 3rd-order nonlinear optical effect. If we use a 2nd-order nonlinear medium, a pump photon is annihilated and a photon pair is created through spontaneous parametric downconversion (SPDC). With a 3rd-order medium, two pump photons are annihilated and a photon pair is created by spontaneous four-wave mixing (SFWM). In both cases, two photons are always generated simultaneously, and we call these photons a photon pair. Hereinafter, one photon of the pair is called the signal and the other is called the idler.

To generate time-bin entangled photon pairs, we input coherent double pulses into a nonlinear medium as a pump. If the pump power is small and the probability that the two pulses will generate photon pairs simultaneously is very low, we can obtain a state consisting of the coherent superposition of the photon-pair state generated by the 1st pulse and that generated by the 2nd pulse. This state can be expressed as

where |X_y denotes a quantum state having a photon in the Xth time slot in mode y (s: signal, i: idler). This state shows a correlation in the measurement that distinguishes the photon's temporal position. Moreover, a correlation is also observed in a measurement that is nonorthogonal to the temporal measurement of the photon. One such measurement distinguishes whether a photon is a superposition of the |1_y and |2_y states with relative phase 0 ((|1_y+|2_y)/) or π ((|1_y–|2_y)/ ).

NTT has succeeded in generating 1.5-µm-band entangled photon pairs by SFWM in optical fibers [1], [2] and silicon wire waveguides [3] and by SPDC in periodically poled lithium niobate (PPLN) waveguides [4]. The setup for entanglement generation using optical fiber [2] is shown in Fig. 1(a). We generated time-bin entangled photon pairs by SFWM in an optical fiber pumped by a double pulse whose temporal interval was 1 ns. The generated photons were separated into signal and idler photons by an optical filter. Then, each photon was launched into a 1-bit delay-line interferometer (an optical interferometer whose two optical paths have a length difference that corresponds to the temporal difference between two pulses). One of the output ports of each interferometer was connected to a single-photon detector. By adjusting the phase difference (φy) between the interferometer's two paths, we can achieve a measurement that detects a photon with quantum state (|1_y+e^–iφy|2_y). We used silica-waveguide-based interferometers in which the phase difference could be tuned by changing the substrate temperature. By measuring both photons in this way, we can investigate the correlation between photons in terms of phase difference. The experimental results are shown in Fig. 1(b). Here, the × symbols denote the idler photon count rate when we swept the phase difference of the idler interferometer. We did not observe any significant variation in the idler count rate, which means that the phase difference was not predetermined. We then swept the phase difference of the idler interferometer while fixing that of the signal interferometer and measured the coincidence rate between two photons. The results are denoted by squares: they show a clear sinusoidal modulation. Thus, we experimentally confirmed the characteristic of entangled photon pairs: the state of each photon is not fixed but the relationship between two photons is predetermined.

Fig. 1. Time-bin entanglement generation experiment. (a) Setup and (b) experimental results.

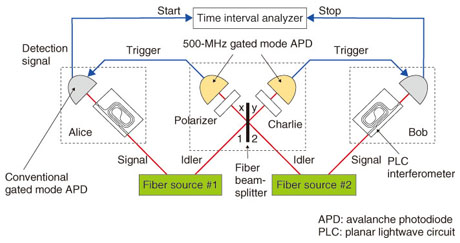
3. QKD using entangled photon pairs

We can implement QKD using entangled photon pairs. We place an entangled photon pair source between two users (Alice and Bob). One photon from the pair is sent through an optical fiber to Alice and the other is similarly sent to Bob. Alice and Bob have instruments for performing two nonorthogonal measurements. They measure each photon with a measuring instrument chosen randomly from the two. With time-bin entangled photon pairs, we can use a time measurement that discriminates state |1_y from state |2_y and a phase measurement to distinguish (|1_y+|2_y)/ ) from (|1_y–|2_y)/ as the two nonorthogonal measurements. These measurements are implemented by using a 1-bit delay-line interferometer and two single-photon detectors that are connected to the output ports of the interferometer. In collaboration with the National Institute of Standards and Technology (NIST), Stanford University, and the National Institute of Information and Communications Technology (NICT), NTT has successfully performed a long-distance QKD experiment using time-bin entangled photon pairs [5]. We used a high-purity time-bin entangled photon pair source based on a PPLN waveguide and superconducting single-photon detectors and achieved secure quantum key distribution over 100 km of fiber.

4. Towards quantum networking: entanglement swapping experiment

In theory, by using an entanglement-based QKD scheme, we can roughly double the key distribution distance compared with that obtained with conventional QKD without entangled photons. However, the distance is still limited by the photon loss caused by the transmission fiber. It is considered difficult to achieve a key distribution distance exceeding 1000 km using current optical fibers as the transmission medium. A quantum repeater is expected to overcome this distance limitation. One key technique for a quantum repeater is entanglement swapping. In this section, I describe an entanglement swapping experiment that was undertaken in the 1.5-µm telecommunications band [6].

The experimental setup, which is shown in Fig. 2, includes two entanglement sources, an intermediate node between the sources (referred to as Charlie), and two users: Alice and Bob. The entanglement sources are based on SFWM in optical fibers pumped by a 500-MHz pump pulse train. These sources generate sequential time-bin entangled photon pairs, whose quantum state is given by

Here, subscripts 1 and 2 indicate that the states originated from sources 1 and 2, respectively. As shown in Fig. 2, the idler photons from the two sources were sent to Charlie through optical fibers, while the signal photons from source 1 (2) were sent to Alice (Bob). Alice, Bob, and Charlie performed coincidence measurements on the kth and (k+1)th time slots, where k is a natural number between 1 and N. The state of the two idler photons was therefore a mixed state composed of the following four states.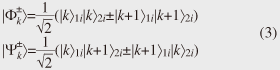

These four are all maximally entangled states known as Bell states. We can transform Eq. (2) by using these four Bell states to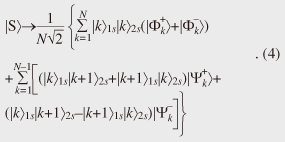

Here, terms that do not contribute to the coincidence measurement between the kth and (k+1)th slots are omitted for simplicity.

Fig. 2. Setup for entanglement swapping experiment.

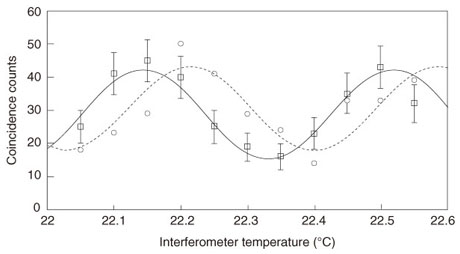
The idler photons that arrived at Charlie were input into a fiber coupler having two input/output ports. The idler photon from source 1 (2) was input into port 1 (2) of the coupler, and the two output ports were denoted ports x and y. These ports were connected to single-photon detectors whose gate frequency was as high as 500 MHz. With current technologies, there is no way to distinguish which of the four Bell states the two incoming idler photons were in. However, it is relatively easy to implement a measurement to show that the incoming state was |Ψ_k^– by using a fiber coupler followed by two single-photon detectors. It can be shown that the incoming photons were in the |Ψ_k^– state if the two idler photons were output from different ports of the coupler and both were counted by the detectors. According to Eq. (5), the state of the two signal photons sent to Alice and Bob is projected to an entangled state (|k_1s|k+1_2s–|k+1_1s|k_2s)/. Thus, by extracting events where two idler photons were observed to be in the Bell state |Ψ_k^–, we can entangle the two signal photons generated in two independent fibers that were originally uncorrelated. This procedure is called entanglement swapping.

We performed coincidence measurements similar to the one described in section 2 under the condition that the two idler photons were measured as being in the |Ψ_k^– state at Charlie. The results are shown in Fig. 3. As we swept the temperature of Bob's interferometer, we observed a clear sinusoidal modulation in the coincidence counts. Thus, we confirmed that two signal photons generated in two independent sources were entangled.

Fig. 3. Results of entanglement swapping.

To date, we have achieved only one-stage entanglement swapping using two sources. As a natural extension, we will try to achieve multistage entanglement swapping using three or more sources. In this way, we should be able to significantly extend the entanglement distribution distance.

5. Future work

By implementing QKD using an entangled state distributed by entanglement swapping, we can, in theory, extend the key distribution distance. However, in reality, since the probability of generating a photon pair at each source is not 100%, the probability of successful entanglement swapping decreases exponentially if we perform multistage entanglement swapping. Therefore, although it is theoretically possible to extend the entanglement distribution distance, the entanglement generation rate may be very small. Consequently, it is very difficult to construct a useful QKD system based on simple entanglement swapping.

We can solve this problem by using a quantum memory that stores the quantum state of light. A quantum memory is a device in which the quantum state of a photon is transferred to another quantum system such as an atom. Then, after the state has been stored for a while, we can convert it back to a photon state at an arbitrary time. This technique should let us improve the success probability of multistage entanglement swapping in the following way. When we succeed in entanglement swapping at a link, we store the entangled photons in quantum memories placed at the link's edge until an entanglement is generated at the adjacent links by entanglement swapping. Then, we convert the photons in the adjacent memories back to photons that engage in another round of entanglement swapping. Thus, we can avoid the exponential decay of the entanglement generation rate. This quantum communication scheme based on entanglement swapping using entangled states stored in quantum memories is called a quantum repeater, and it is expected to be an essential scheme for achieving global-scale quantum communication. Many institutions, including NTT, are currently undertaking research aimed at achieving quantum repeaters.

References

[1]	H. Takesue, "Generation of Polarization-entangled Photon Pairs in 1.5-μm Telecommunication Band," NTT Technical Review, Vol. 3, No. 12, pp. 52–60, 2005. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr200512052.pdf
[2]	H. Takesue and K. Inoue, "Generation of 1.5-μm Band Time-bin Entanglement Using Spontaneous Fiber Four-wave Mixing and Planar Lightwave Circuit Interferometers," Phys. Rev. A, Vol. 72, No. 4, p. 041804, 2005.
[3]	H. Takesue, K. Harada, Y. Tokura, H. Fukuda, T. Tsuchizawa, T. Watanabe, K. Yamada, and S. Itabashi, "Entanglement Generation Using Silicon Wire Waveguide," NTT Technical Review Vol. 8, No. 2, 2010. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201002sf6.html
[4]	H. Takesue, K. Inoue, O. Tadanaga, Y. Nishida, and M. Asobe, "Generation of Pulsed Polarization-entangled Photon Pairs in a 1.55-μm Band with a Periodically Poled Lithium Niobate Waveguide and an Orthogonal Polarization Delay Circuit," Opt. Lett., Vol. 30, No. 3, pp. 293–295, 2005.
[5]	T. Honjo, S. W. Nam, H. Takesue, Q. Zhang, H. Kamada, Y. Nishida, O. Tadanaga, M. Asobe, B. Baek, R Hadfield, S. Miki, M. Fujiwara, M. Sasaki, Z. Wang, K. Inoue, and Y. Yamamoto, "Long-distance Entanglement-based Quantum Key Distribution over Optical Fiber," Opt. Express, Vol. 16, No. 23, pp. 19118–19126, 2008.
[6]	H. Takesue and B. Miquel, "Entanglement Swapping Using Telecom-band Photons Generated in Fibers," Opt. Express, Vol. 17, No. 13, pp. 10748–10756, 2009.

↑ TOP