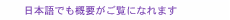Network Reliability Optimization by Using Binary Decision Diagrams

1. Network reliability

Communication networks have become a key infrastructure and so must work without failure. However, network components such as links and nodes may fail for several reasons. Since these failures are inevitable, communication networks must be designed so that they continue to function even if these failures occur. How can we design such networks?

An example of a simple communication network is shown in Fig. 1(a). Since the network connects two terminals with one link, the network will fail if the link fails. In contrast, a network with an additional link is shown in Fig. 1(b). This network will continue to work if one of the links fails. Therefore, this network is more reliable than the single-link network.

Fig. 1. Communication network examples. Network (b) is more robust against link failures than network (a).

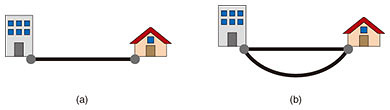
Network reliability is a measure used for quantifying how robust a communication network is against failures. It is defined as the probability that the network will continue to support communications assuming that the failure of its components follows some probabilistic distributions.

Let us compute the network reliabilities of the networks in Fig. 1. We assume that each link fails independently with a probability of 20%. Since the probability of the network in Fig. 1(a) working equals the probability that the link between terminals works, its network reliability is 80%. In contrast, the network in Fig. 1(b) will continue to work unless both links fail simultaneously. Since the probability of such an event happening is 20% × 20% = 4%, the reliability of the network is 96%. In this way, network reliability can quantify the robustness of a communication network. We note, however, that evaluating network reliability is a computationally difficult problem and becomes infeasible for large networks.

2. Network reliability maximization

If a communication network is assessed to have sufficient reliability, we can continue to use it without modification. If, however, the reliability is insufficient, remedial action is needed. A typical approach is adding links to the network since that always improves the reliability. The task of finding the best way to add links to improve reliability can be formulated and solved as the combinatorial optimization^*1 problem called the network reliability maximization problem. In what follows, we make the realistic assumption that the total budget for adding links to the network is limited, and we want to maximize network reliability under this budget constraint. We call this problem the budget constrained network reliability maximization problem.

The input of this optimization problem is a communication network that consists of nodes and links, the total budget, and a set of candidate positions for adding new links. We assume that for each candidate position, the cost for adding a link to the position, and the probability that the added link will fail are known in advance. The output of the problem is the communication network topology that achieves the maximum network reliability score and satisfies the constraint that the total cost incurred in adding links does not exceed the budget. An example of a budget constrained network reliability maximization problem and the set of candidate solutions of the problem are respectively shown in Figs. 2 and 3. Of the candidate solutions shown in Fig. 3, the center one is the optimal solution—the communication network topology that achieves the maximum reliability among those satisfying the budget constraint.

Fig. 2. Budget constrained network reliability maximization problem.

Fig. 3. Example solutions for the problem in Fig. 2. The network in the center is an optimal solution.

We have seen that we can design a communication network that is robust against failures by solving the network reliability maximization problem. However, this problem is known to be computationally hard; it takes a prohibitively long time even if we exploit powerful modern computers.

A straightforward approach to solve the network reliability maximization problem is to first enumerate all candidate network topologies that can be made while satisfying the budget constraint and then evaluating the network reliability of each candidate. However, this simple approach has two potential problems. First, the number of candidate topologies satisfying a constraint may grow exponentially with network size. Second, evaluating the reliability of a candidate solution also takes an exponential amount of time. To evaluate the reliability of a network, we must enumerate all the possible link failure patterns with which the network works. Since the number of such failure patterns grows exponentially with network size, the computation time also grows exponentially. Due to these two difficulties, previous methods can find optimal solutions only for very small networks, that is, networks with fewer than 20 nodes.

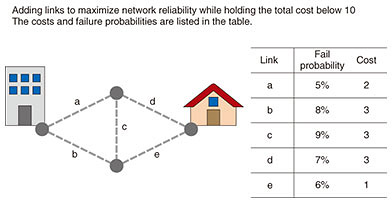
3. Efficient optimization with binary decision diagrams

We propose an efficient algorithm^*2 for finding the optimal solutions of budget constrained reliability maximization problems [1]. This algorithm can find optimal solutions for communication networks with more than 100 nodes. It can handle networks that are 10 times the size of those possible with previous methods. Moreover, the proposed method works more than 10 thousand times faster than existing methods. The key to our algorithm is that it uses the data structure called binary decision diagrams (BDDs) [2].

BDDs can represent a set of failure patterns in a compressed form. We show in Fig. 4 a communication network (Fig. 4(a)) and its possible failure patterns where the network still survives (Fig. 4(b)). In Fig. 4(c), we show a BDD representing the set of failure patterns in Fig. 4(b). A BDD is a directed graph that consists of two types of vertices—the circles and rectangles in the figure. Every circle vertex has two arcs—a solid arc and a dashed arc—and is associated with a link of the communication network in Fig. 4(a). Every rectangle vertex has a label of either 1 or 0 and they are placed at the bottom.

Fig. 4. Using a BDD to represent failure patterns.

In the BDD shown, every failure pattern in Fig. 4(b) corresponds to a directed path in the BDD from the root BDD vertex to the rectangle terminal vertex with label 1. We can obtain the path that corresponds to a failure pattern in the following way; given a failure pattern, we first select the root BDD vertex (say v). Then we check the link associated with the label of v. If the link works in the failure pattern, we follow the solid arc and update v to the node reached. Otherwise, if the corresponding link fails in the current failure pattern, we follow the dashed arc of v and update v to the node reached.

By repeatedly updating v depending on its labels, we obtain a path in the BDD. For example, the failure pattern marked by the green circle in Fig. 4(b) corresponds to the path on the BDD represented by the green arrow. By representing each failure pattern as a path, the BDD can share equivalent partial paths and thus represent the set of paths in a succinct way. For example, the BDD in Fig. 4(c) represents 16 failure patterns as a directed graph with 10 vertices. Since we need 5 vertices for each failure pattern if they are represented as paths, the compression ratio of this BDD is 12.5%. When the input network is large, the compression rate is smaller.

By using a BDD to compress the set of failure patterns, we can accelerate some of the computations needed in solving budget constrained network reliability maximization problems. First, we can accelerate network reliability evaluation. By using a BDD, we can precisely evaluate network reliability in time linear to the number of BDD vertices. If the compression ratio of a BDD is 99%, just 1% of the original computation cost is needed to evaluate network reliability. Second, a BDD can be used to estimate the amount of improvement that can be achieved by adding a link to the network. Such estimations allow us to efficiently discard candidate network topologies that may not achieve high reliability. This can also reduce the computation cost needed to find an optimal solution. In this way, BDDs enable us to optimize the reliability of large communication networks.

Up to this point we have focused on the problem of maximizing network reliability under budget constraints. In the real world, another design goal is to achieve reliability higher than a given threshold value at minimum cost. Our algorithm can be applied to this problem and can efficiently find the minimum cost solution.

4. Conclusion

We have introduced an efficient algorithm that can find network topologies that maximize network reliability. This algorithm can be applied to designing infrastructure networks in addition to communication networks such as road networks, rail networks, and power transmission networks, all of which demand high reliability. Of course, we have to consider several aspects other than reliability when designing communication networks. The most reliable network might not be the best one if other aspects are considered. Future work includes enhancing our optimization method so that it can simultaneously handle multiple aspects, one of which is reliability.

References

[1]	M. Nishino, T. Inoue, N. Yasuda, S. Minato, and M. Nagata, “Optimizing Network Reliability via Best-first Search over Decision Diagrams,” Proc. of the IEEE International Conference on Computer Communications (INFOCOM 2018), pp. 1817–1825, Honolulu, HI, USA, Apr. 2018.
[2]	R. E. Bryant, “Graph-based Algorithms for Boolean Function Manipulation,” IEEE Transactions on Computers, Vol. C-35, No. 8, pp. 677–691, 1986.