|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Feature Articles: Encryption and Security Technologies for Creating a Safe and Secure Society Vol. 19, No. 6, pp. 88–93, June 2021. https://doi.org/10.53829/ntr202106fa14 Security Based on Quantum Information Technology and Data Protection of Quantum InformationAbstractQuantum information processing is expected to have unique security applications such as communication security and copy protection based on physical principles in addition to high-speed computation. For the practical use of quantum information processing, fault-tolerant processing is essential to protect quantum information from noise, and fault-tolerant processing for quantum communication based on quantum repeaters is the key for networking. We introduce our efforts in this area in this article. Keywords: quantum information processing, security, fault-tolerant technology 1. IntroductionThe possibility of new high-speed computation using quantum information processing has been attracting attention, and new security using such processing and data protection of quantum information are also important research topics. Quantum information is known to be very sensitive to noise, and to process information correctly, it is necessary to protect quantum information from noise and errors. Protecting the availability of such information processing is one of the three elements of security*, and is one of the important roles of security. Without this, no matter how fast the computation is or how many new security applications there are, the information cannot be processed correctly. The ability to protect quantum data from noise is the most important issue in quantum information processing, and the security of quantum information processing supports the backbone of such processing. The possibility for new security using quantum information processing is, in a sense, to take advantage of this weakness against noise, but the nature of quantum states is such that if one touches a quantum state to eavesdrop or forge it, traces as noise will inevitably be left behind. Quantum cryptography takes advantage of this property to detect eavesdroppers and maintain security in principle. (Quantum cryptography is also called quantum key distribution because it is usually used to distribute secret keys.) The nature of quantum states can also be used to prevent counterfeiting and has potential applications in quantum money and quantum copyright protection, where counterfeiting by copying is impossible in principle. Such functions will become more valuable when quantum networks are enhanced; therefore, it is necessary to develop quantum repeaters and construct a large-scale quantum network. Since quantum communication is also vulnerable to loss and noise, the ability to protect data from noise in quantum communication can be regarded as the security of such communication. In this article, we first introduce quantum error correction and quantum error mitigation, which are two important technologies for protecting quantum information data. We then discuss copy protection as a new application possibility and finally introduce research on quantum repeaters, which is a fundamental technology for quantum networks.
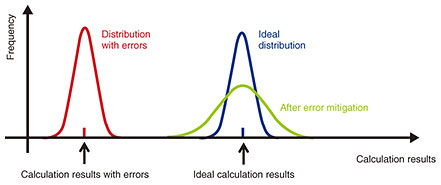
2. Fault-tolerant technology to protect quantum information dataIn many applications of quantum information processing, error rates during computation must be sufficiently small. Quantum error correction is a technology that can significantly reduce effective error rates by encoding the information of qubits using multiple noisy qubits and by detecting and correcting errors sequentially. Building a fault-tolerant quantum computer (FTQC) [1], which enables fault-tolerant quantum information processing using quantum error correction, is one of the most promising ways to demonstrate practical applications in a scalable manner. However, it is not easy to build an FTQC with practical performance because quantum error correction requires many qubits, feedback, and other complicated processing [2]. Therefore, to build a useful FTQC, it is necessary to research and develop an efficient architecture from software to hardware by considering many trade-off relations and performance bottlenecks. We are working on the research and development of software infrastructure for building a practical FTQC. Specifically, we are developing a method of quantum error correction for distributed computing systems [3], method for optimizing decoding circuits for small codes by machine learning [4], circuit design of peripheral devices for low-latency decoding algorithms [5], calibration method for accurate control of integrated qubits [6], framework for high-speed measurements of qubits, and series of fundamental software to comprehensively evaluate and improve the accuracy of these methods. Near-term quantum computation has attracted a great deal of attention. This is because in October 2019, Google announced that it was able to solve a very specific, impractical problem, which was said to take a very long time to solve with existing computers, by using a 53-qubit quantum computer. Researchers worldwide are studying how to make practical use of such quantum devices and applications such as machine learning and chemical calculations. However, to exploit the computational power of such small-scale quantum computers, it is necessary to suppress computational errors. Quantum error correction has been studied for many years for removing computational errors, but this method uses qubits as a resource for error suppression, which is incompatible with small-scale quantum devices that can be fabricated now or in the near future due to the limited number of qubits. Instead, quantum error mitigation (or quantum noise compensation) has been proposed as an alternative to suppressing errors without (significantly) increasing the number of qubits, and a number of papers have been published recently. Quantum error mitigation is a method for effectively suppressing computational errors by adding error-suppression operations to the quantum algorithm then executing existing classical information processing on the readout measurement results (Fig. 1). In this case, the resource required for quantum error mitigation is a larger number of measurements (number of calculations). For error mitigation, there is an overhead of larger number of samples, thus it is not scalable. Nevertheless, it has been shown that error mitigation can effectively suppress errors if the frequency of computational errors is small in the quantum algorithm [7]. Our group has also recently shown that the number of qubits required for FTQC can be reduced in a practical manner by incorporating quantum-error-mitigation methods into FTQC, indicating that quantum error mitigation is a method with a wide range of applications [8].
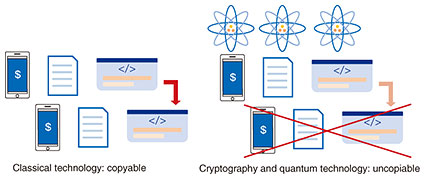
3. Secure copy protection from cryptography and quantum information technologyThere are various topics at the intersection of cryptography and quantum information processing. Technology related to these two fields are roughly categorized into (1) cryptography secure against quantum computers (post-quantum cryptography) [9], (2) quantum cryptography, which uses quantum information processing to achieve secure communication [10], and (3) cryptography with new functionalities that can be achieved by using only quantum information processing. The main theme of this section is about (3), but we briefly explain (1) and (2). Post-quantum cryptography does not require the power of quantum information processing or quantum computers, but it is designed to guarantee its security even against quantum computers. Quantum cryptography requires the power of quantum information processing or quantum computers to achieve cryptographic functionalities, but its functionalities are the same as those of classical cryptography. For example, we can achieve secure encrypted communication without the power of quantum information theory, but we can enhance security by using this power. In contrast, (3) is cryptography with new functionalities that cannot be achieved without using the power of quantum information theory. A typical example is data copy protection or software copy protection (Fig. 2).
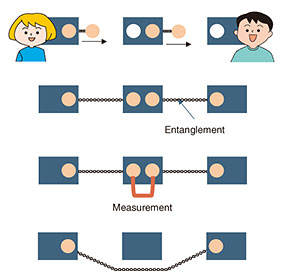
We can generate an unbounded number of copies of digital data. It is impossible to prevent the copying of digital data and software. However, this is the case in which we do not consider quantum information technology. In quantum information theory, there exists a no-cloning theorem that states that copying an unknown quantum state is impossible [11, 12]. By applying this theorem to cryptography, we might be able to achieve data copy protection or software copy protection. Currency is a type of data that we want to prevent from being copied. Quantum money was proposed as currency that can never be copied [13, 14]. Since current software is digital data, it is hard to prevent software piracy in principle and there is no copy-protection method that guarantees security. Provably secure software copy protection [14] makes it impossible to generate a copy of software by using cryptography and quantum technology. Achieving secure software copy protection is one of our goals. Copy-protection techniques have many applications other than quantum money and secure software copy protection. For example, it is possible to securely delete (encrypted) data that were stored in a cloud storage and prevent the cloud from reconstructing the data [15]. It might be possible to securely implement the right to be forgotten (General Data Protection Regulation [16] Article 17). It is possible to lease software in a limited time and make the functionality unavailable after the software was returned [17]. Our group is conducting research and development to achieve cryptography with new functionalities above what can be achieved by using only the power of quantum information [18]. 4. Quantum repeater technologies for quantum networksCurrent computation and communication technologies are all based on the rules of classical physics and can only execute computation and communication within the limits of classical physics. The same is true for security. We can currently provide only security within the limits of classical physics, but we can expand the possibilities of security by using quantum mechanics. For example, we enable eavesdropper detection in key distribution [19] and an information-theoretically secure and simple secure computing protocol that uses only one server [20]. It is known that the resource for such quantum mechanical effects as communication is a correlation unique to quantum mechanics called entanglement. To make security applications based on quantum mechanics available on a global scale, it is necessary to create entanglement and construct quantum networks in which entanglement can be shared over long distances and in multiple locations (Fig. 3).
If we want to share the entanglement over long distances, we cannot use conventional relaying methods because simple amplification is not possible due to the property of quantum states; quantum states cannot be copied. Since the probability of direct transmission becomes exponentially smaller due to losses, a method of relaying entanglement distribution is required. The following is a brief description of the main points of the method. First, the direct transmission distance can be shortened by placing repeaters at a distance that does not cause large loss, thereby reducing the loss. However, a certain amount of loss and error is unavoidable, so multiple communications are executed redundantly at each repeater point, and a process equivalent to quantum error correction is applied to them to enable transmission with reduced loss and error. This is a fault-tolerant processing of entanglement communication and is called entanglement distillation (purification) because it is the process of extracting near-perfect entanglement from multiple noisy entanglements. Our group is working on constructing quantum repeaters using ultra-low loss nano-fiber cavities [21]. The ultra-low loss nano-fiber cavity consists of two elements: an ultra-low loss tapered fiber and ultra-low loss fiber Bragg grating. We are investigating methods of improving the performance of the quantum memory by using it as follows. By trapping atoms, which are used as quantum memory, in the vicinity of a tapered fiber, which is much thinner than an ordinary fiber, we can enable photons through the tapered fiber and atoms to interact. By placing the entire repeater system inside the fiber, it is possible to reduce optical loss by eliminating the lossy process of emitting photons out into free space to interact with atoms. By using a cavity structure with a fiber Bragg grating, it is also possible to increase the probability that photons emitted from the quantum memory will be coupled into the fiber. This will increase the success probability of write and read operations on the quantum memory, improving the overall performance of the repeater. The realization of quantum networks using high-performance quantum repeaters will provide various security applications, including those for diplomacy and defense, handling genetic information, and financial institutions. 5. ConclusionIt is important to emphasize once again that fault-tolerant and quantum repeater technologies, which protect the data of quantum information and quantum communication, are essential for the correct and safe execution of quantum information processing [22]. There are many unexplored areas of architectures for fault-tolerant processing in quantum information processing, and breakthroughs are expected through future research. For the security applications of quantum information processing, in addition to secure secret communication and copy protection, new applications such as quantum-secure computation and quantum-based reduction of communication complexity are expected. Near-term quantum security, which is not yet so large in scale, is also a promising research theme. References
|
|||||||||||||||||||||||||||||||||||||||||||||||