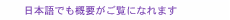Machine Learning That Reproduces Physical Phenomena from Data

1. Machine learning and physics simulation

The dynamics of many physical phenomena are described with differential equations. Traditionally, experts in various fields have designed equations to reproduce physical phenomena through observation and theoretical investigation (top of Fig. 1). Solving these equations can simulate physical phenomena under various conditions using a computer without real-world experiments. Physical simulations are used in various real-world applications, such as weather forecasting and aircraft design. However, the design of equations is very costly, and there are limitations in modeling complex phenomena, such as weather, in the real world.

Fig. 1. Differences in approaches.

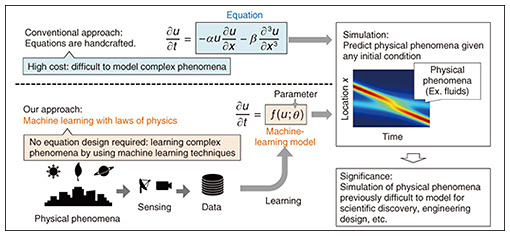
Advances in information and communication technologies have attracted attention to data-driven approaches. Machine learning has revealed that various real-world problems can be solved with extremely high accuracy by using large-scale data.

Is it possible to simulate physical phenomena using machine learning? To answer this question, my research colleagues and I are studying machine-learning models for accurately reproducing physical phenomena from observed data. Unlike the conventional approach of handcrafting differential equations described above, we are developing a model for automatically constructing a highly accurate physics simulator from data without the need to design equations for the phenomena (bottom of Fig. 1).

2. Limitations of current machine-learning models

Behind the data-driven approach for physics simulation was a technological breakthrough: Neural ordinary differential equation (NODE) [1], published in 2018. NODE uses observed data to learn the neural-network parameters to represent a phenomenon without designing an equation (see the orange box “Machine-learning model” in Fig. 1).

Is it possible to simulate physical phenomena by naively applying NODE to observed data? Unfortunately, achieving a highly accurate simulation is difficult. Figure 2 shows the results of an experiment using a pendulum as an example of a simple physical system. We provide the dynamics of a pendulum in the upper center of Fig. 2, with the angle on the horizontal axis and the angular momentum on the vertical axis. Due to the energy conservation law, the black dot (i.e., the system’s state) continues to move in the green orbit. Given the observed data of such motion (upper right of Fig. 2), the simulation result using NODE is the lower part of Fig. 2. The simulated trajectory deviates from the true orbit depicted in green. The simulation accuracy significantly degrades when only a small amount of data containing a large amount of noise is available.

Fig. 2. Limitations of current machine-learning models.

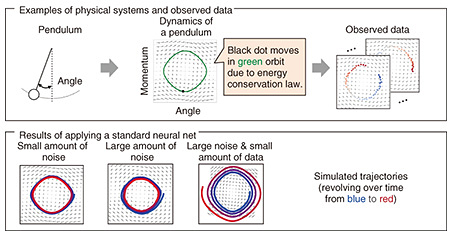
3. Difficulty in learning

Why did we obtain these results? Machine-learning models are known to be highly expressive and have the potential to accurately model large and complex physical phenomena. Due to their high expressive power, it is not easy to identify a model that accurately reproduces a physical phenomenon from the vast search space of machine-learning models (the gray region in Fig. 3). Learning becomes even more difficult when only a small amount of data containing a large amount of noise or missing values is available.

Fig. 3. Narrowing down search space via prior knowledge.

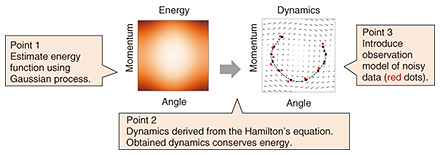
4. Introducing prior knowledge of physics

When data are scarce containing a large amount of noise or missing values, it is effective to introduce prior knowledge that can provide hints to guide appropriate learning. The research field that aims to use prior knowledge from physics for training is called physics-informed machine learning [2] and has been gaining attention. It is expected to narrow the search space and effectively identify models that accurately reproduce physical phenomena (see orange region in Fig. 3). The simplest way to introduce prior knowledge is to assume an equation, as with the conventional approach illustrated in Fig. 1, and learn the physical parameters (α and β in Fig. 1) in the equation from the data. However, this approach narrows the search space too much. It does not take advantage of the high expressive power of machine-learning models, making it difficult to apply to complex phenomena that cannot be represented with known equations. Therefore, we focused on using the laws of physics as prior knowledge. This enables us to maintain the expressive power of the machine-learning model while appropriately narrowing the search space.

5. Machine-learning model incorporating the energy conservation law

Throughout history, various physical laws have been discovered, including conservation of energy, conservation of mass, and conservation of momentum. I introduce a case study of incorporating the energy conservation law, which is generally obeyed in dynamical systems, into a machine-learning model. The theory of Hamiltonian mechanics is a convenient way to describe physical phenomena that obey the energy conservation law. In Hamiltonian mechanics, instead of designing equations that represent physical phenomena, the energy function of the physical system is designed. Once the energy function is determined, the physical dynamics can be systematically obtained in accordance with the Hamilton’s equation. It should be noted that the dynamics derived from the Hamilton’s equation can be guaranteed to always obey the energy conservation law. The Hamiltonian neural network (HNN) [3] was proposed to train a model for estimating from data the physical phenomena that follow the energy conservation law by replacing the energy function with a neural network. With neural-network-based models, however, it is implicitly assumed that data of sufficient quality and quantity are available. When such data are unavailable, the models often over-fit to the data, resulting in a loss of accuracy. Therefore, we developed a Gaussian-process model [4] incorporating the theory of Hamiltonian mechanics. The Gaussian process is a machine-learning model advantageous for learning from a small amount of data with a large amount of noise. Figure 4 shows a schematic diagram of this model. The model has the following three features. The first feature is estimating the energy function by a Gaussian process instead of a neural network. This is expected to avoid overfitting and estimate the energy function even when the amount of data used for training is small. The second feature is deriving the dynamics using the Hamilton’s equation. It can be guaranteed that the Gaussian process will always satisfy the energy conservation law. The third feature is introducing an observation model for noisy data. This enables robust learning even from noisy data. Our model enables effective learning of physical phenomena that obey the energy conservation law, even when data of insufficient quality and quantity are available and enables highly accurate simulations.

Fig. 4. Our Gaussian-process model.

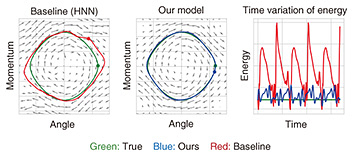
Figure 5 shows the results of simulating the motion of a pendulum using the conventional model (i.e., HNN) and our model. From comparing the left and middle of Fig. 5, our model is more accurate in simulating the true trajectory (in green). The right of Fig. 5 plots the energy variation over time. The true value (in green) is constant due to the energy conservation law. Our model captures the energy value more accurately than the conventional model. These results indicate that our model accurately simulates physical phenomena while obeying the energy conservation law.

Fig. 5. Simulation results.

6. Prospects and applications

There are still limitations in the input data required for training and the types of physical phenomena that can be handled. We will aim to reproduce more complex phenomena on the basis of more realistic observations for real-world applications. In the research introduced in this article, we assumed that physical variables, such as the angle of a pendulum, can be observed. However, as physical systems become more complex, it is not easy to obtain such variables directly. However, sensor values, images, and videos related to physical phenomena may be relatively easy to observe. We need a technology that can reproduce physical phenomena even when such types of inputs are given. In addition, complex real-world phenomena, such as meteorological phenomena, are often represented with a partial differential equation, and it is desirable to extend the technology to such equations.

As this research field develops, it is expected to have a variety of applications. For example, weather forecasting can address environmental issues, such as climate change, or reproduce phenomena such as typhoons and tsunamis for disaster prevention. The simulation of complex weather phenomena in the real world, which cannot be represented with manually crafted equations, is expected to provide more accurate forecasting. Aircraft, automobiles, semiconductors, and other products are designed using physics simulation. If physics simulators can be automatically acquired from observed data, it will be possible to make simulators more accurate and efficient when creating new products. A simulator can also be applied to artificial-intelligence tasks, such as scene understanding by robots. For example, when a human sees an image of a messy stack of packages, they can infer that it may collapse. If robots can learn physical phenomena using the ideas in this research, we believe it will be possible for them to avoid risks in such situations.

This work was supported by Japan Science and Technology Agency (JST), ACT-X Grant Number JPMJAX210D, Japan.

References

[1]	R. T. Q. Chen, Y. Rubanova, J. Bettencourt, and D. K. Duvenaud, “Neural Ordinary Differential Equations,” Advances in Neural Information Processing Systems 31 (NeurIPS 2018), 2018.
[2]	G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang, “Physics-informed Machine Learning,” Nat. Rev. Phys., Vol. 3, No. 6, pp. 422–440, 2021. https://doi.org/10.1038/s42254-021-00314-5
[3]	S. Greydanus, M. Dzamba, and J. Yosinski, “Hamiltonian Neural Networks,” Advances in Neural Information Processing Systems 32 (NeurIPS 2019), 2019.
[4]	Y. Tanaka, T. Iwata, and N. Ueda, “Symplectic Spectrum Gaussian Processes: Learning Hamiltonians from Noisy and Sparse Data,” Advances in Neural Information Processing Systems 35 (NeurIPS 2022), 2022.