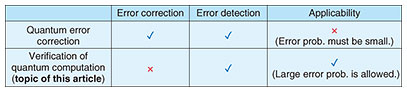
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Feature Articles: Designing a Future Where Everyone Can Flourish by Sharing Diverse Knowledge and Technologies

Vol. 21, No. 10, pp. 26–29, Oct. 2023. https://doi.org/10.53829/ntr202310fa4

Dilemma between Quantum Speedup and Computational Reliability—Overcoming Errors with Efficient Verification Methods for Quantum Computing

Yuki Takeuchi and Seiichiro Tani

Abstract

Quantum computers are expected to solve several problems faster than any classical computer. However, they may sometimes output incorrect answers because they are prone to errors. Therefore, to develop reliable quantum computers, it is essential to develop methods of verifying whether the outputs of quantum computers are correct. In this article, we introduce our recent research results on our verification methods.

Keywords: quantum computer, cloud quantum computing, quantum information processing

1. Advantages and issues with quantum computers

In 1994, Shor proposed a quantum algorithm that efficiently factors large integers [1]. It is strongly believed that factorization is a hard problem for classical computers, and this hardness conjecture is used as evidence of the security of several modern cryptographic protocols. Shor’s algorithm is a well-known instance showing the computational advantage of quantum computers, and since his proposal, quantum computers have been extensively studied. The quantum computational advantage is known for several problems, such as the simulation of physical and chemical systems and the approximation of Jones polynomials. Despite these advantages, quantum computers face implementation challenges due to environmental noise. There are various methods for designing qubits; a qubit is the basic unit of information in quantum computers. When superconducting circuits are used as qubits, for example, errors can occur due to temporal fluctuations in the resonant frequency. In factorization, such errors are not significant. This is because the correctness of the output (i.e., the answer to a factorization) can be easily checked by executing multiplication on a classical computer; hence, it is easy to determine whether errors have occurred during the quantum computation. As mentioned above, quantum computers can also be applied to various problems other than factorization. For instance, when using a quantum computer to approximate Jones polynomials, there is no known classical method for efficiently checking whether the output is an accurate approximation. In other words, there is a dilemma caused by quantum superposition. This enables high-speed calculations of quantum computers but makes it difficult to verify the correctness of the outputs. To leverage the high computational power of quantum computers, it is necessary to address the impact of errors and develop techniques for resolving this dilemma.

2. Techniques to protect quantum computers from errors

This section discusses two techniques to suppress the impact of errors during quantum computations: quantum error correction and mitigation and verification of quantum computation. Quantum error correction is a technique that detects and corrects errors. The information of a single qubit is encoded using multiple physical qubits. Since it is currently challenging to prepare a large number of physical qubits, the implementation of quantum error correction is still limited to small-scale experiments. To overcome this limitation, quantum error mitigation has been proposed, which suppresses the impact of errors by repeating small-scale quantum computations instead of increasing the number of qubits. However, quantum error mitigation is applicable only to limited tasks, such as calculating expectation values, and generally requires an exponential number of executions of quantum computations. To apply quantum error correction or mitigation, some knowledge about the errors is required. Several quantum-error-correction protocols and quantum-error-mitigation methods cannot be used unless the error probability is sufficiently small.

Verification of quantum computation can be used even when the error probability is large. However, it cannot correct or mitigate errors; it can only detect errors. By solving the same problem multiple times with a quantum computer and verifying each answer, it is possible to extract the correct answers, i.e., the output that is not affected by errors. Therefore, verification can be considered effective for addressing the impact of errors.

As a summary, quantum error correction can correct errors but is applicable to limited situations with small error probabilities. Verification of quantum computation, however, can be used even when error probabilities are large but can only detect errors. Quantum error correction thus compensates for the verification drawbacks and vice versa. Therefore, both techniques are crucial for developing highly reliable large-scale quantum computers (see Table 1). In the following sections, we introduce some of our research results on our methods for verifying quantum computation.

Table 1. Quantum error correction and verification of quantum computation.

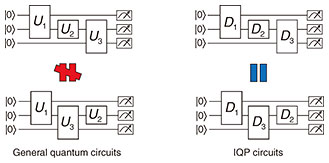
3. Several verification methods

3.1 Verification of measurement-based quantum computation

There are several models of quantum computing. One is measurement-based quantum computation (MBQC). In the conventional approach known as the quantum circuit model, quantum computation is executed by first initializing qubits then applying quantum gates to them, followed by measurements. In MBQC, once a specific entangled state^* called a graph state is prepared, any quantum computation can be carried out by sequentially measuring individual qubits. Since the graph state is independent of the problems to be solved, it can be prepared in advance before starting to solve the problems. When we design qubits by using light (more precisely, photons), single-qubit gates and measurements are relatively easy to conduct. However, the implementation of two-qubit operations is challenging and can only be done probabilistically (in linear optical quantum computing). In MBQC, two-qubit gates are only required during the preparation of the graph state. After starting to solve the problems, only simple operations, i.e., measurements, are needed. This is a significant advantage over the quantum circuit model. Therefore, MBQC has been applied to various quantum-information-processing tasks such as quantum cryptography and quantum communication.

When a quantum computer is developed in accordance with MBQC, the step of preparing a graph state is the most error-prone. Therefore, several methods have been proposed for verifying whether the graph state is correctly prepared. In 2019, we devised an efficient verification method, which was superior in efficiency to other verification methods at that time [2]. To achieve this improvement, we were the first to apply a mathematical technique, which was previously used in quantum key distribution, to verification. Subsequently, we applied our verification method to quantum sensing [3] and experimentally demonstrated it in a small-scale optical experiment [4]. These developments indicate a significant impact and expansion of our research in this field.

3.2 Verification of quantum-random-number generation

We extended the graph-state verification mentioned in the previous section to more complex quantum states called weighted graph states. This extension enables the verification of a family of quantum circuits called instantaneous quantum polynomial-time (IQP) circuits. This family of circuits can only execute a limited set of computations obtained regardless of the order of quantum gates to be applied (see Fig. 1), although this property may make the physical implementation of IQP circuits easier. Consequently, the computational power of IQP circuits should be weaker than that of an ideal full-fledged quantum computer since the computation on the latter heavily depends on the order of quantum gates. By using ideal IQP circuits, however, it is possible to generate random numbers that is difficult on classical computers. It is not easy to determine whether the generated numbers follow an ideal probability distribution or noisy one that is easily reproducible with classical computers. In 2019, we made it possible to efficiently check whether the random numbers are correctly generated by conducting verification of IQP circuits [5].

Fig. 1. IQP and general quantum circuits.

3.3 Verification of noisy intermediate-scale quantum computers

Quantum computers with computational capabilities weaker than full-fledged quantum computers, such as IQP circuits, are referred to as non-universal quantum computers. Some non-universal quantum computers are currently in use or expected to be developed in the near future. They are called noisy intermediate-scale quantum (NISQ) computers, which are small or medium-scale quantum computers with inevitable noise. As reviewed in another article in this journal [6], we proposed a verification method tailored for NISQ computers [7].

3.4 Verification of quantumness of quantum computers

Our methods introduced above require small-scale quantum measurement devices to execute verification. In other words, these methods verify the outputs of various quantum computers, such as MBQC, IQP circuits, and NISQ computers, by using another smaller quantum computer. To make verification of quantum computation more practical, it would be desirable to enable efficient verification using a classical computer. In 2018, Mahadev proposed a classical verification method [8] by using post-quantum cryptography, which is modern cryptography secure even against quantum attacks. Her method was a significant breakthrough in the field and was subsequently extended by many researchers. In 2022, by applying her technique, we also proposed a verification method for verifying the correct preparations and measurements of a special quantum state, so-called magic state [9]. Quantum computation without magic states (specifically, computations limited to Clifford unitary operations) can be efficiently simulated with classical computers. Therefore, verifying magic states can be used to determine the presence of essential quantum properties in quantum computers.

*	Entangled state: A quantum state with quantum correlation. It can be generated using two or more qubits. It plays an essential role in various quantum-information-processing tasks.

4. Outlook

We proposed various verification methods that make several types of quantum computers verifiable. Further improvements in many directions are necessary for their practical use. A possible direction would be to improve our methods and apply verification of quantum computation to cloud-quantum-computing systems. Companies, such as IBM and Amazon, provide cloud-quantum-computing systems, but they lack the verification features for users to check the correctness of their received results. By incorporating verification methods into existing systems, users can verify the accuracy of their received answers for themselves, and the companies providing the systems can transparently demonstrate the high performance of their quantum computers. Our goal is to achieve a society where anyone can benefit from quantum computers from anywhere. Toward this goal, we will continually contribute to the development of fundamental technologies in quantum computing.

References

[1]	P. W. Shor, “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer,” SIAM J. Comput., Vol. 26, 1484, 1997. https://doi.org/10.1137/S0097539795293172
[2]	Y. Takeuchi, A. Mantri, T. Morimae, A. Mizutani, and J. F. Fitzsimons, “Resource-efficient Verification of Quantum Computing Using Serfling’s Bound,” npj Quantum Information, Vol. 5, 27, 2019. https://doi.org/10.1038/s41534-019-0142-2
[3]	Y. Takeuchi, Y. Matsuzaki, K. Miyanishi, T. Sugiyama, and W. J. Munro, “Quantum Remote Sensing with Asymmetric Information Gain,” Phys. Rev. A, Vol. 99, 022325, 2019. https://doi.org/10.1103/PhysRevA.99.022325
[4]	P. Yin, Y. Takeuchi, W.-H. Zhang, Z.-Q. Yin, Y. Matsuzaki, X.-X. Peng, X.-Y. Xu, J.-S. Xu, J.-S. Tang, Z.-Q. Zhou, G. Chen, C.-F. Li, and G.-C. Guo, “Experimental Demonstration of Secure Quantum Remote Sensing,” Phys. Rev. Applied, Vol. 14, 014065, 2020. https://doi.org/10.1103/PhysRevApplied.14.014065
[5]	M. Hayashi and Y. Takeuchi, “Verifying Commuting Quantum Computers via Fidelity Estimation of Weighted Graph States,” New J. Phys., Vol. 21, 093060, 2019. https://doi.org/10.1088/1367-2630/ab3d88
[6]	S. Tani, S. Akibue, and Y. Takeuchi, “Extracting Quantum Power by Using Algorithms and Their Verification,” NTT Technical Review, Vol. 21, No. 6, pp. 43–47, 2023. https://doi.org/10.53829/ntr202306fa5
[7]	Y. Takeuchi, Y. Takahashi, T. Morimae, and S. Tani, “Divide-and-conquer Verification Method for Noisy Intermediate-scale Quantum Computation,” Quantum, Vol. 6, 758, 2022. https://doi.org/10.22331/q-2022-07-07-758
[8]	U. Mahadev, “Classical Verification of Quantum Computations,” SIAM J. Comput., Vol. 51, 1172, 2022. https://doi.org/10.1137/20M1371828
[9]	A. Mizutani, Y. Takeuchi, R. Hiromasa, Y. Aikawa, and S. Tani, “Computational Self-testing for Entangled Magic States,” Phys. Rev. A, Vol. 106, L010601, 2022. https://doi.org/10.1103/PhysRevA.106.L010601

Yuki Takeuchi: Associate Distinguished Researcher, Computing Theory Research Group, Media Information Laboratory, NTT Communication Science Laboratories.
He received a Ph.D. in science from Osaka University in 2018. He joined NTT Communication Science Laboratories as a research associate the same year and was a researcher from 2019 to 2023. Since April 2023, he has been in his current position and engaged in the theoretical investigation of quantum information and is especially interested in the verifiability of quantum computing. He received IPSJ Computer Science Research Award for Young Scientists from the Information Processing Society of Japan (IPSJ) and Young Scientist Award of the Physical Society of Japan from the Physical Society of Japan. He is a member of the Physical Society of Japan and IPSJ.

Seiichiro Tani: Distinguished Scientist, Computing Theory Research Group, Media Information Laboratory, NTT Communication Science Laboratories.
He received a B.E. in information science from Kyoto University in 1993 and M.E. and Ph.D. in computer science from the University of Tokyo in 1995 and 2006. He joined NTT LSI Laboratories in 1995 and moved to NTT Network Innovation Laboratories in 1998. Since 2003, he has been studying quantum computing theory at NTT Communication Science Laboratories. He is also an associate member of the Science Council of Japan and visiting professor at the Quantum Computing Unit, International Research Frontiers Initiatives (IRFI), Tokyo Institute of Technology. He was a member of ERATO/SORST Quantum Computing and Information Project, Japan Science and Technology Agency (JST) from 2004 to 2009 and visiting researcher at the Institute for Quantum Computing (IQC), the University of Waterloo, Canada, from 2010 to 2011. He received the Institute of Electronics, Information and Communication Engineers (IEICE) Achievement Award and the IEICE Information and Systems Society Best Paper Award. He also received the Maejima Hisoka Award. He is a member of the Association for Computing Machinery (ACM), the Institute of Electrical and Electronics Engineers (IEEE), IEICE, and IPSJ.

↑ TOP