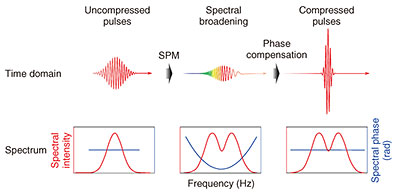
Megahertz-repetition-rate 1.7-cycle Intense Pulse Sources for Future Bright Attosecond Spectroscopy

1. Toward the future of attosecond spectroscopy

The conferral of the 2023 Nobel Prize in Physics for the generation of attosecond light pulses remains vivid in our recollection [1]. An attosecond pulse has an extremely short duration within the attosecond range (10^–18 seconds), typically ranging the spectra between the extreme ultraviolet and soft X-ray regions. By using these attosecond pulses as “a flash of stroboscopic imaging,” ultrafast phenomena occurring on the attosecond timescale can be dynamically observed. These time-resolved spectroscopies are crucial for investigating electron dynamics in materials [2] and chemical reaction processes.

The underlying principle of attosecond pulse generation is high-order harmonic generation (HHG) [3, 4], a process that transpires when intense pulses (driver sources) are directed onto atoms. Electrons within atoms are usually bound by the Coulomb potential of the nucleus. However, when an intense pulse, with a field strength comparable to 1 V/Å, irradiates an atom, the Coulomb potential is distorted, leading to the tunneling ionization of electrons. Since the optical field is an AC (alternating current) filed, the electrons undergo a U-turn during the subsequent half-cycle and return to their parent nuclei. During this re-collision, light with frequencies that are integer multiples of the driver source (harmonics) is emitted. This constitutes the principle of HHG and the fundamental mechanism underlying attosecond pulse generation.

For attosecond time-resolved spectroscopy, pulses with attosecond duration are indispensable. As described above, attosecond pulses are produced at each half-cycle of the driver source. While each attosecond pulse is generated with attosecond precision, the resultant output forms a pulse train resembling a “bundle,” exhibiting a temporal structure closely aligned with the pulse duration of the driver source. Consequently, the temporal resolution achieved does not attain attosecond precision. To achieve attosecond time-resolved spectroscopy, isolating the attosecond pulses is crucial. A representative approach to accomplish this is shortening the pulse duration of the driver source to a few cycles (typically fewer than two cycles) and stabilizing the optical-field shape. To generate an isolated attosecond pulse, the optical-field shape must be fixed to a cosine waveform.

This technology necessitates highly advanced and sophisticated techniques, unattainable with conventional commercial laser systems. NTT Basic Research Laboratories has pioneered research in isolated attosecond pulse generation, culminating in the first observation of petahertz-scale (hundreds of attoseconds) electronic oscillations in solids [2].

However, attosecond spectroscopies have long been hindered by a significant challenge: the low photon flux of attosecond light pulses. This limitation arises from the low conversion efficiency of HHG, typically ranging from 10^–6 to 10^–8. The primary determinant of the photon flux of attosecond pulses is the driver source. Attosecond pulses have traditionally been generated using titanium-sapphire amplifiers operating at kHz-repetition rates, with average powers of only a few watts. Recently, ytterbium (Yb) amplifiers have emerged as alternative driver sources due to their ability to be directly pumped by laser diodes and their high quantum efficiency. These Yb amplifiers facilitate high-average-power operation at the 100-W level with MHz-repetition rates. We thus anticipate generating attosecond pulses at MHz-repetition rates, leading to significantly brighter attosecond spectroscopies. Our objective is to harness this enhanced brightness to develop next-generation attosecond spectroscopic technologies and investigate previously uncharted ultrafast phenomena on the attosecond timescale.

2. Few-cycle compression at 80-W-class average power

The generation of few-cycle pulses with high average power is important yet challenging. While Yb amplifiers are capable of delivering high average output, they cannot be directly used as an attosecond driver source for isolated attosecond pulse generation due to long pulse durations ranging from several picoseconds to several hundred femtoseconds. To overcome this limitation, pulse compression techniques are applied to reduce the pulse duration to the few-cycle regime. In the time domain, short optical pulses are achieved by coherently superimposing spectral components within a specific frequency range. A critical consideration is that there exists a fundamental limit, beyond which the pulse duration cannot be further shortened, even when all spectral phases are aligned within a defined spectral band—this is referred to as the Fourier-transform limit. Therefore, to generate few-cycle pulses, it is essential to first broaden the spectrum of the original pulses.

To broaden the spectrum, self-phase modulation (SPM) is commonly used. This phenomenon arises from the temporal modification of the refractive index as a function of pulse intensity, i.e., the nonlinear refractive index. When a laser pulse is incident on a medium, SPM occurs due to the pulse’s own optical field. This results in a lower frequency in the first half of the pulse and higher frequency in the second half (Fig. 1, center). This modulation generates a new frequency component, thereby broadening the spectrum. By adjusting the spectral phase of the broadened optical pulse to achieve phase alignment at each frequency, a shorter pulse duration can be attained (Fig. 1, right). This process is referred to as pulse compression.

Fig. 1. Schematic of pulse compression.

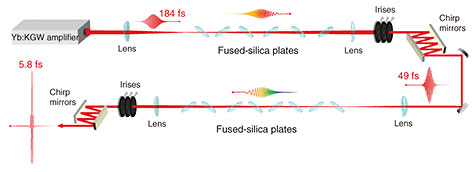
In this study, laser light from a Yb:KGW amplifier with a high average power of 80 W (energy: 80 µJ, center wavelength: 1035 nm, pulse width: 184 fs) was compressed into a few-cycle pulse under 1-MHz-repetition-rate operation [5]. Solid materials with strong nonlinear effects were selected as the medium for the SPM in the pulse compressor. Specifically, six thin fused silica plates were placed to broaden the spectrum. By applying this compressor in two stages, we aimed to achieve few-cycle pulses (Fig. 2). The first stage was used to broaden the spectrum to 960–1100 nm at the 10^–3 level via the SPM, and the unbroadened higher-order modes were removed with an iris. The resulting spectrum is almost symmetrically broadened with a reduced spectral density at the center wavelength of 1035 nm, which is typical tendency of SPM. This tendency predicted that compensation of group-delay dispersion would be sufficient for phase compensation. Therefore, we compensated the compressed pulses with −1600 fs², resulting in a compression to 49 fs.

Fig. 2. Illustration of the pulse compressors.

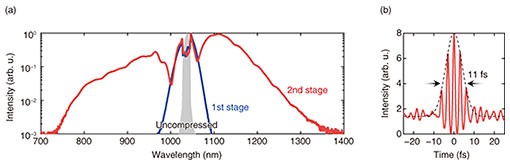
The compressed pulse was further compressed to obtain few-cycle pulses. Eight fused silica plates were used to broaden the spectrum to an octave band ranging from 700 to 1400 nm at the 10^–3 level (Fig. 3(a)). After eliminating higher-order modes through spatial filtering, the pulses were compressed by phase compensation using a −300-fs² chirped mirror and 2-mm-thick glass. The compressed pulse was then measured using a fringe-resolved autocorrelation interferometer, yielding a full width at half maximum of 11 fs (Fig. 3(b)). Assuming the waveform follows a sech² shape, this pulse width corresponds to 5.8 fs, which translates to 1.7-cycle pulses when referenced to the 1035-nm center wavelength of the original laser source. This 1.7-cycle pulse represents the shortest duration of an attosecond driver source operatable at a MHz-repetition-rate operation.

Fig. 3. Experimental results of compressed pulses. (a) Spectrum before and after spectral broadening. (b) Autocorrelation of the 1.7-cycle pulses.

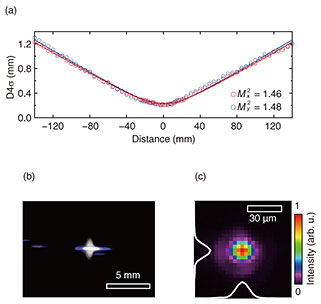
We verified the applicability of this 1.7-cycle pulse for isolated attosecond pulse generation. The critical criterion for this application is the intensity of the pulses that can be focused per unit area. To evaluate this, we assessed the spatial quality and focusing performance. Specifically, the M² was determined using a beam diameter of D4σ on the basis of the ISO 11670 standard. We measured the position dependence of D4σ with focusing components, resulting in M² of 1.46 and 1.48, respectively (Fig. 4(a)). This performance is considered standard for few-cycle pulses and expected to be suitable for attosecond pulse generation.

When the 1.7-cycle pulse was focused intensely with a parabolic mirror with a 10-cm focal length, plasma emission was observed in air (Fig. 4(b)). This luminescence primarily originated from nitrogen, which has an ionization energy comparable to that of argon, a gas typically used for attosecond pulse generation. These findings suggest the potential for attosecond pulse generation with argon. For a more quantitative evaluation, we confirmed that the 1/e² beam diameter achieved an intensity of 7.1 × 10¹⁴ W/cm². Given that a focused intensity above 10¹⁴ W/cm² is required to ionize argon, we conclude that these 1.7-cycle pulses can be effectively used for attosecond pulse generation.

Fig. 4. Focusing quality. (a) M² measurement. (b) Photograph of plasma in the air. (c) Focused beam profile at (b).

3. Conclusion and future outlook

We have introduced the MHz-repetition-rate generation of a 1.7-cycle intense pulse source by combining an Yb amplifier with pulse compression. The next milestone is to stabilize the carrier-envelope phase to attain an unprecedented bright isolated attosecond pulse. Our study will open new avenues for advanced attosecond time-resolved spectroscopies, such as attosecond imaging, polarimetry, and microscopy.

We thank Prof. Ming-Chang Chen of National Tsing Hua University for his helpful comments and suggestions. This research was partially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 20H05670.

References

[1]	Nobel Prize in Physics 2023, https://www.nobelprize.org/prizes/physics/2023/summary/
[2]	K. Oguri, “Attosecond Time-resolved Spectroscopy for Light-electron Interaction in Solid-state Materials,” NTT Technical Review, Vol. 23, No. 5, pp. 29–35, May 2025. https://ntt-review.jp/archive/ntttechnical.php?contents=ntr202505fa4.html
[3]	P. B. Corkum, “Plasma Perspective on Strong Field Multiphoton Ionization,” Phys. Rev. Lett., Vol. 71, No. 13, 1994. https://doi.org/10.1103/PhysRevLett.71.1994
[4]	M. Ferray, A. L’Huillier, X. F. Li, L. A. Lompre, G. Mainfray, and C. Manus, “Multiple-harmonic Conversion of 1064 nm Radiation in Rare Gases,” J. Phys. B: At. Mol. Opt. Phys., Vol. 21, No. 3, pp. L31–L35, 1988. https://doi.org/10.1088/0953-4075/21/3/001
[5]	T. Okamoto, Y. Kunihashi, Y. Shinohara, H. Sanada, M. C. Chen, and K. Oguri, “Operation at 1 MHz of 1.7-cycle Multiple Plate Compression at 35-W Average Output Power,” Opt. Lett., Vol. 48, No. 10, pp. 2579–2582, 2023. https://doi.org/10.1364/OL.477372