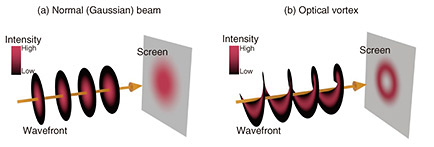
Topological High-harmonic Generation from Solids

1. Control of topological wavefronts of light via high-harmonic generation

The ability to control key parameters of laser light, such as wavelength (frequency), intensity, phase, polarization, and wavefront shape, has led to applications across diverse fields, including optical communications, science, industry, and medicine. Recent advances in the study of light-matter interactions under intense laser irradiation have contributed to technologies such as laser processing and wavelength conversion. Wavelength conversion is essential for generating laser light at desired wavelengths, and at NTT Basic Research Laboratories (NTT BRL), we are investigating high-harmonic generation (HHG) as a type of wavelength conversion.

HHG occurs when an intense femtosecond laser pulse^*1 is irradiated onto a medium, producing not only commonly used second- and third-harmonic generation but also much higher-order harmonics (integer multiples of the frequency). This phenomenon underlies the generation of attosecond optical pulses, a breakthrough that won the 2023 Nobel Prize in Physics [1].

Despite its significance, HHG-related technologies are still in their early stages of development. At NTT BRL, we have been studying HHG for many years, achieving control over fundamental optical parameters such as frequency, intensity, and phase through pulse shortening, wavelength extension, and power enhancement. Our current goal is to further control the remaining key parameters—polarization and wavefront—to enable complete manipulation of all optical properties of HHG.

At NTT BRL, we focus on circular polarization and optical vortices as key properties for characterizing laser light’s polarization and wavefront (Fig. 1). Circular polarization has two helicities (s = −1 or +1), representing the fundamental degree of freedom in polarization control. The topological charge of light describes its spatial mode and is associated with orbital angular momentum. While conventional laser beams exhibit a Gaussian beam^*2 wavefront, it is also possible to generate beams with a helical wavefront, known as topological light. The topological charge (l = … −2, −1, 0, 1, 2, …) determines the number and direction of wavefront rotations. Optical vortices in the visible, infrared, and radio-wave regions have been applied to optical multiplexing, microscopic spectroscopy, optical tweezers, and laser processing [2–5].

Fig. 1. Wavefront of the optical vortex and intensity distribution of the beam cross-section when it hits the screen.

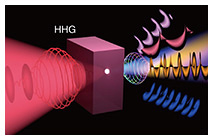
If similar wavefront control can be achieved in HHG, it would enable wavelength conversion into the vacuum and extreme ultraviolet (XUV) regions—wavelengths that are difficult to produce directly with lasers. This could lead to novel applications such as nanometer-scale spectroscopy and lithography for ultrafine measurement and processing. However, controlling light in the XUV range is challenging because of the difficulty in fabricating optical components for such short wavelengths. Instead of modifying the harmonics after generation, an alternative approach is to control the polarization and wavefront of the laser before HHG. However, a unified understanding of how these properties transform during HHG has been lacking due to the complex physics involved.

To address this challenge, we successfully demonstrated simultaneous control of polarization and wavefront shape in HHG by leveraging the symmetry^*3 of solid-state crystals (Fig. 2) [6]. We found that the conversion rules governing these properties are fundamentally dictated by crystal symmetry. This discovery establishes a universal principle for predicting the polarization and wavefront characteristics of harmonics generated through solid-state materials, marking a significant advancement in fundamental optical technology.

Fig. 2. The generation of high-harmonic light in an optical vortex state when circularly polarized light is irradiated onto a solid crystal.

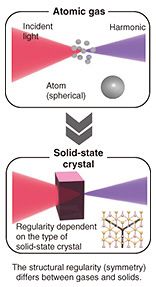
2. Solid-state HHG using symmetry

When controlling the polarization and wavefront shape of light generated through wavelength conversion, symmetry provides an effective approach. Symmetry refers to the property of a physical system that remains unchanged under specific transformations. By focusing on dynamical symmetry^*4, which characterizes the spatiotemporal structure of both electromagnetic waves and solid-state crystals, we can achieve HHG while preserving the regularity of polarization and wavefront shape before and after wavelength conversion. While this does not allow for complete arbitrary control, it enables the selective generation of well-defined optical states such as circularly polarized light and optical vortices.

Traditionally, gases have been the primary medium for generating high-harmonic orders beyond the second and third harmonics. However, in gases, individual atoms are randomly distributed in space, making it impossible to systematically control the polarization or wavefront of the generated harmonics by simply changing the gas type. In this study, we used solid-state crystals, leveraging their intrinsic symmetry arising from the regular atomic arrangement to control light properties (Fig. 3). The categorized symmetry of different solids allows for the selective generation of well-defined optical states on the basis of simple rules.

Fig. 3. Differences in media for HHG.

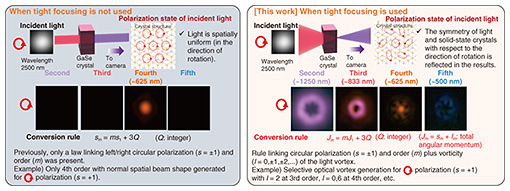
The application of crystal symmetry in HHG was previously limited to controlling polarization. For example, when circularly polarized fundamental light is irradiated onto a solid crystal with discrete rotational symmetry, high harmonics of different orders (second, third, fourth, etc.) are selectively emitted with either left- or right-handed circular polarization, determined by the crystal’s rotational symmetry [7]. In our study, we extended this principle beyond polarization to include wavefront, demonstrating a new degree of control over HHG.

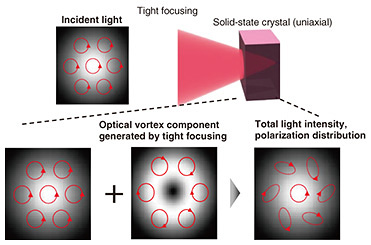
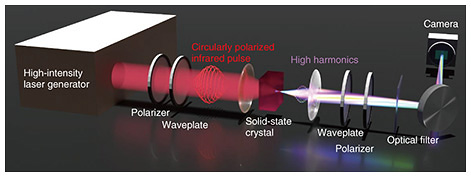
3. Generation of topological light via circular polarization conversion

We devised an optical experimental system that enables the simultaneous control of not only circular polarization, which is relatively easy to manipulate in solid-state HHG, but also optical vortex states. By tightly focusing a circularly polarized Gaussian beam using a short-focal-length lens onto a thick uniaxial crystal^*5, we observed the generation of optical vortex components. This process creates a spatially structured polarization distribution within the material, enabling the formation of unique polarization states inside the crystal (Fig. 4).

Fig. 4. The polarization state of light tightly focused onto a solid crystal using a short-focal-length lens.

The generation of these optical vortex components occurs due to birefringence induced by tight focusing. When the beam is tightly focused, certain components enter the crystal at an oblique angle relative to its thickness, causing them to undergo birefringence^*6. This mechanism allows for the simple generation of optical vortices without requiring specialized optical elements while simultaneously enabling HHG within the same solid-state crystal.

A crucial aspect of this process is that the resulting electromagnetic field profile exhibits well-defined symmetry. Specifically, the combined symmetry of polarization, wavefront, and the solid-state crystal ensures the simultaneous control of both the polarization and wavefront of the generated harmonics. This, in turn, enables the derivation of a simple conversion rule (equation) that defines the relationship between polarization, wavefront shape, and harmonic order.

4. Topological HHG and optical conversion laws

We experimentally demonstrated the control of topological HHG using the symmetry of solid-state crystals and, for the first time, verified the optical conversion rules governing this process. Our observations confirmed that various wavelengths of light generated through HHG exhibit controlled circular polarization and optical vortex states. In our experiment, we generated a circularly polarized Gaussian beam using an intense infrared femtosecond laser with a wavelength of 2500 nm. The beam was tightly focused onto a 2-mm-thick uniaxial gallium selenide (GaSe) crystal using a 6-mm focal length lens to induce HHG (Fig. 5). The emitted harmonics, spanning red, orange, and blue wavelengths, were separated according to their polarization components. By capturing the resulting beams with a camera, we analyzed their spatial profiles. The results revealed that harmonics of various wavelengths, including red, orange, and blue, were generated, and their beam shapes depended on both wavelength and polarization (Fig. 6).

Fig. 5. Optical experimental system for HHG.

Fig. 6. Captured spatial-beam profiles of high-harmonics (showing only the harmonics of one circular polarization component) and the conversion rule.

A comparison between tight focusing and loose focusing showed significant differences in the spatial distribution of infrared polarization within the solid crystal, leading to markedly different harmonic beam profiles. Under loose focusing, the generated harmonics followed conventional rules governing harmonic order and polarization, producing only Gaussian beam profiles. In contrast, tight focusing resulted in distinct donut-shaped and windmill-shaped beam profiles. The donut shape, observed in the third harmonic, corresponds to a single optical vortex state, whereas the windmill shape, seen in the fourth harmonic, indicates the simultaneous generation of multiple optical vortices. These results confirm that tight focusing facilitates the transformation of circular polarization into optical vortex components, generating multiple harmonic components with nonzero topological charge.

By considering symmetry in our experimental setup, we derived a simple equation governing the transformation of optical angular momentum in HHG:

where m represents the harmonic order, n is the rotational symmetry index of the crystal, Q is an integer, and J_m = s_m + l_m denotes the total angular momentum, with s_m representing helicity and l_m representing topological charge. This equation, which can be regarded as a conservation rule for total optical angular momentum, indicates that the angular momentum^*7 of light remains conserved before and after wavelength conversion.

We used right-handed circularly polarized light (s₁ = 1) with a Gaussian beam profile (l₁ = 0) as the incident beam, and the GaSe crystal exhibited threefold rotational symmetry in the beam cross-section (n = 3). Under these conditions, the total angular momentum J_m for each harmonic order was determined within the integer range of Q, enabling us to predict the polarization state (s_m) and topological charge (l_m) of the harmonics. The experimentally observed spatial profiles matched these theoretical predictions exactly, demonstrating successful simultaneous control of circular polarization and optical vortex states.

While GaSe was used in this experiment, the approach is universally applicable to other solid-state crystals. By selecting different crystals or modifying the incident beam’s wavefront shape, it is possible to adjust n and J₁ in the equation, thus precisely controlling the polarization direction and topological charge of the generated harmonics. This optical conversion rule provides a fundamental principle for controlling the polarization and wavefront shape of high harmonics, serving as a key theoretical framework for future advancements in HHG-based optical manipulation.

5. Conclusion and future outlook

This study introduced an approach to generating topological optical waves through HHG and presented the world’s first experimental demonstration of the fundamental rules governing this process. The conversion rule derived from symmetry has broad applicability and, under the right conditions, represents a universal principle that nonlinear optical phenomena should obey. Just as the rule of energy conservation, which also arises from symmetry, is a fundamental principle governing our physical world, the rule we discovered provides a general framework for understanding light-conversion processes induced by intense laser fields. Applying this principle to the control of spatial modes in high-harmonic UV light could pave the way for advancements in ultrafast spectroscopy, lithography, and other cutting-edge measurement technologies in the UV regime.

This research was partially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 20H05670.

References

[1]	Nobel Prize in Physics 2023, https://www.nobelprize.org/prizes/physics/2023/summary/
[2]	J. Wang, J.-Y. Yang, I. M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. Ren, Y. Yue, S. Dolinar, M. Tur, and A. E. Willner, “Terabit Free-space Data Transmission Employing Orbital Angular Momentum Multiplexing,” Nat. Photon., Vol. 6, pp. 488–496, 2012. https://doi.org/10.1038/nphoton.2012.138
[3]	K. I. Willig, S. O. Rizzoli, V. Westphal, R. Jahn, and S. W. Hell, “STED Microscopy Reveals that Synaptotagmin Remains Clustered after Synaptic Vesicle Exocytosis,” Nature, Vol. 440, No. 7086, pp. 935–939, 2006. https://doi.org/10.1038/nature04592
[4]	M. Padgett and R. Bowman, “Tweezers with a Twist,” Nat. Photon., Vol. 5, pp. 343–348, 2011. https://doi.org/10.1038/nphoton.2011.81
[5]	K. Toyoda, K. Miyamoto, N. Aoki, R. Morita, and T. Omatsu, “Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures,” Nano Lett., Vol. 12, No. 7, pp. 3645–3649, 2012. https://doi.org/10.1021/nl301347j
[6]	K. Nagai, T. Okamoto, Y. Shinohara, H. Sanada, and K. Oguri, “High-harmonic Spin-orbit Angular Momentum Generation in Crystalline Solids Preserving Multiscale Dynamical Symmetry,” Sci. Adv., Vol. 10, No. 31, 2024. https://doi.org/10.1126/sciadv.ado7315
[7]	N. Saito, P. Xia, F. Lu, T. Kanai, J. Itatani, and N. Ishii, “Observation of Selection Rules for Circularly Polarized Fields in High-harmonic Generation from a Crystalline Solid,” Optica, Vol. 4, No. 11, pp. 1333–1336, 2017. https://doi.org/10.1364/OPTICA.4.001333