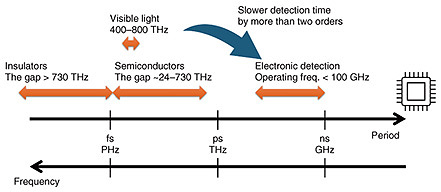
Exploring Ultrafast Electron Dynamics and Extreme Nonlinear Optics Induced by Intense Optical Field

1. Ultrafast electron dynamics induced by intense optical fields and their theoretical description

At NTT Basic Research Laboratories, we are engaged in fundamental research to elucidate the fundamental aspect of light-matter interactions. For this study, we explored the physical limits of optoelectronic interconversion.

Semiconductors typically have a band gap in the range of 0.1–3 eV, which corresponds to a frequency range of 24–730 THz when converted using Planck’s constant h = 4.136 eV/PHz (or equivalently, a period of 42–1.4 fs, where fs = 10^–15 s) (Fig. 1). When light is irradiated onto a semiconductor, excitation of electrons occurs, leading to rapid oscillations within the material with a period of several femtoseconds, corresponding to the band-gap energy. However, when attempting to detect these electronic excitations induced by light, the detection frequency typically drops below several hundred gigahertz (corresponding to a period of 10 ps or longer, where ps = 10^–12 s). The primary reasons for this include the need to transport excited electrons from the reaction center to the detection region and the frequency limitations of the electronics used. We aim to observe and control the oscillations of photoexcited electrons in semiconductors and insulators on a femtosecond (or in some cases, attosecond) timescale, thereby exploring the fundamental limits of optoelectronic interconversion. In other words, our research seeks to answer a fundamental question: How fast can light and matter interact?

Fig. 1. Time constants of light-matter interaction and electronics.

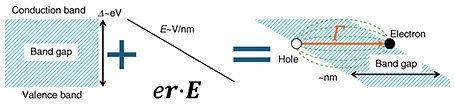
How can we investigate extremely fast optical responses of 1 eV (i.e., h/(4.136241 fs))? The most common method is the pump-probe method, which compresses light with photon energies above 1 eV into an ultrashort pulse with a duration of several femtoseconds and sets the peak of the pulse envelope as the time zero for the optical response. The pump-probe method enables the observation of the effect of the first pulse by adjusting the delay time between two pulses and measuring the response of the second pulse. The shortest achievable pulse width is on the order of the carrier-wave oscillation period. We focused on a different approach: ultrafast electron dynamics induced by high-amplitude optical fields via tunneling effects. This phenomenon is governed by the amplitude of the oscillating electric field, with the time zero defined at the zero crossing of the oscillating field. A key characteristic of this approach is that the response is dominated by dynamics faster than the carrier frequency (which corresponds to the photon energy). Such phenomena are also referred to as sub-cycle dynamics by light.

When a high-intensity electric field is applied to a semiconductor or insulator with an energy gap, electrons in the valence band can transition to the conduction band via quantum tunneling. When an electric field E is applied, an electron exhibits a potential eEx (where e > 0). This potential causes the valence and conduction bands to develop an energy gradient of eE (Fig. 2). As E increases, the forbidden energy gap becomes thinner, and once it reaches a sufficiently thin state, electrons can tunnel through, leading to dielectric breakdown. The tunneling-transition rate per unit time Γ can be approximately expressed using the lattice constant a, effective mass μ, and band-gap energy Δ [1, 2]:

Fig. 2. Tilting of the band gap in a material under an applied electric field. Electrons and holes created across the narrowed band gap exhibit Coulomb interaction.

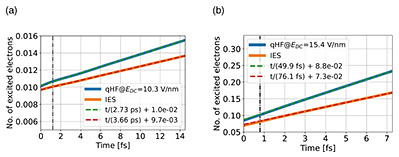
Although this expression simplifies the situation and is not necessarily exact, it is useful for rough estimates. For quartz, where μ = 0.347, Δ = 9.08 eV, and a = 0.339 nm, an experimentally achievable electric field of 15.4 V/nm yields Γ = 6.57 THz (or equivalently, 1/152 fs). At first glance, 152 fs might seem slow; however, it is important to note that this time constant does not describe the intrinsic motion of electrons but rather the timescale for carrier doping via the optical field. Applying an electric field of 15.4 V/nm results in the introduction of photo-carriers at a rate of 6.57% per 10 fs. Prolonged exposure to such a high-intensity optical field would excite an excessive number of electrons, causing irreversible damage to the material. Therefore, extremely short optical pulses on the order of a few femtoseconds are used in experiments. The crucial timescale for electronic oscillations corresponds to the band-gap energy, meaning that for quartz, charge oscillations at 9.08 eV are induced in the material.

In phenomena induced by actual high-intensity light, processes other than the tunneling effect also occur. Thus, a highly nonlinear response to the applied electric field arises, leading to electron oscillations shorter than the carrier frequency of the light. Therefore, the time constant can drop below the femtosecond range and reach the attosecond scale [3]. The field of research that investigates such ultrafast optical responses induced by intense optical fields is known as extreme nonlinear optics.

Understanding ultrafast and atomic-scale phenomena requires theoretical studies, and quantum mechanical simulations play a crucial role. Experiments in extreme nonlinear optics typically involve applying electric fields on the order of volts per nanometer to semiconductors and insulators for durations of only a few femtoseconds. Direct experimental observations are often limited to macroscopically averaged optical responses over micrometer scales, time-integrated currents accumulated over nanoseconds, or time-resolved photoelectron spectra. However, such data only provide partial snapshots of the phenomena, making their interpretation highly challenging. Thus, theoretical research is essential for unveiling the interactions between light and matter on atomic and femtosecond (or even attosecond) scales, which are beyond the reach of current experimental techniques.

Various theoretical approaches can be used to analyze extreme nonlinear optics, with real-time quantum dynamics simulations being particularly direct and powerful. For instance, when evaluating tunneling-transition rates, a common approach involves approximating the stationary solution of the quantum dynamical equation of motion. However, it is well known that the tunneling-transition rate depends on the assumed form of the stationary solution [2]. A more accurate method involves solving the equation of motion in the time domain and evaluating the tunneling-transition rate as a slope of the stationarity of the numerical solution. In this study, we solved the equations of motion governing electrons while incorporating many-body effects at the mean-field level, enabling us to evaluate the tunneling-transition rate with high precision.

2. Electron-electron interactions in ultrafast electron dynamics

We provide an overview of the theoretical description of electron-electron interactions, which represented the most significant technical challenge in this study.

The theoretical framework for handling electron-electron interactions in solids is well established for static properties, but its validation for time-dependent dynamics remains insufficient. Over the past quarter-century, advances in computational technology have enabled highly accurate reproduction of many static properties of materials—such as the most stable atomic structures, elastic constants, band-gap values, and optical constants—through atomic-scale theoretical calculations. Many of these atomic-scale theoretical calculations, although including approximations, rely solely on fundamental physical constants such as the elementary charge and Planck’s constant, Coulomb forces acting between charges, and quantum mechanics. These calculations are therefore referred to as first-principles calculations, as they do not depend on empirical material-specific parameters. For quantum many-body systems that exhibit time dependence due to external fields such as light, their quantitative validity has not been as thoroughly verified as that of static properties. The main reasons for this are the difficulty in comparing dynamic properties between theory and experiment and the high computational cost of theoretical simulations, which makes solving them fully a significant challenge. “Difficult to solve fully” means that as the simulation size is incrementally increased, the computational cost becomes so large that it is impossible to confirm whether the physical quantities of interest have sufficiently converged with respect to the system size. When a simulation is not fully solved, even when the same equations are used as a starting point, the results can vary depending on the numerical implementation, making it difficult not only to compare different simulations but also verify consistency with experimental results.

We adopted a mean-field approximation that incorporates electron-hole interactions, which are the key interactions in the optical response of semiconductors, and developed a simulation code to solve the quantum dynamics of electrons under a steady electric field. The mean-field approximation used in this study effectively averages out two-body interactions between electrons, incorporating the potential formed by the distribution of all other electrons into a single potential function. This potential is determined self-consistently so that it aligns with the electron distribution obtained from the solutions of individual electronic equations of motion. In the case of Fermions, this method is known as the time-dependent Hartree-Fock (TD-HF) method. The TD-HF method is a theoretical framework that includes electron-hole interactions, which play an extremely important role in the optical response of semiconductors. When an external field, such as light, is applied to a fully occupied valence band, electrons are excited to the conduction band, leaving behind holes in the band. These holes behave as positively charged quasiparticles with charge +e, while the excited electrons have charge –e. The interaction between these electrons and holes is called the electron-hole interaction (see dashed lines in Fig. 2), and its effects are prominently observed in the optical absorption of many semiconductors through the formation of bound electron-hole pairs known as excitons.

We used a mean-field model capable of reproducing experimental values under known conditions to investigate many-body effects. When solving the TD-HF equations, the most computationally expensive component is the calculation of electron-electron interactions, with its cost increasing proportionally to the square of the system size. Consequently, directly solving the three-dimensional Coulomb interaction following first-principles calculations would incur an extremely high computational cost. To mitigate this, we used an effective one-dimensional model. First-principles TD-HF methods are known to overestimate the strength of electron-hole interactions. To address this, we developed a modified TD-HF method called time-dependent quasi-Hartree-Fock (TD-qHF) method, which enables us to adjust the strength of electron-hole interactions so that the exciton binding energy matches experimental values or results from high-precision theoretical calculations. Although this method sacrifices a fully first-principles description, it enables the tuning of parameters such as the band gap and effective mass to match experimental or high-precision theoretical values. This flexibility enables us to selectively include or exclude electron-hole interactions to simulate different aspects of electron dynamics.

The reduced computational cost achieved through model simplifications also enables us to obtain fully converged results with respect to system size, ensuring reliable simulations of ultrafast electron dynamics.

3. Enhancement of tunneling-transition rate due to electron-electron interactions

We investigated the tunneling-transition rate, which describes the rate at which valence electrons escape into the conduction band via the tunneling effect under a high-intensity electric field applied to a crystal [4]. We evaluated how the presence or absence of electron interactions affects the tunneling-transition rate.

Figure 3 shows the time evolution of the number of electrons that transitioned to the conduction band when a steady electric field of 10.3 and 15.4 V/nm was applied to quartz. It is evident that the number of conduction band electrons increases proportionally with time. The tunneling-transition rate is determined from this slope. Increasing the electric field amplitude from 10.3 to 15.4 V/nm, a factor of 1.5, results in an approximately 60-fold increase in Γ, demonstrating strong nonlinearity. Comparing the results of the TD-qHF method with those of the independent electron system (IES), which does not include electron-hole interactions, we found that the tunneling-transition rate is consistently higher in the former. The enhancement factor of the tunneling-transition rate due to electron-hole interactions is 1.33 for 10.3 V/nm and 1.50 for 15.4 V/nm. Additional simulations for other materials showed that, with some exceptions, this enhancement factor generally increases monotonically with the electric field strength [4]. A possible expectation is that as the electric field increases, electron dynamics would become increasingly dominated by kinetic energy, reducing the relative impact of electron-hole interactions [3]. However, our study suggests that this is not necessarily the case.

Fig. 3. Time evolution of the number of electrons transitioning to the Conduction band under a steady electric field applied to a simulated quartz system ((a) 10.3 V/nm, (b) 15.4 V/nm). Results for TD-qHF (solid blue line) and the IES (solid orange line), along with their respective linear fits (dashed green line, dashed red line). Reprinted with permission from Ref. [4]. Copyright 2023 by American Physical Society.

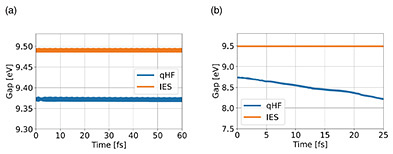
Given that electron-hole interactions enhance the tunneling-transition rate, it is natural to question the underlying mechanism. To clarify this mechanism, we conducted simulations on systems with extremely strong electron-hole interactions and plot the time-dependent changes in the band gap in Fig. 4. For both electric-field amplitudes, TD-qHF calculations show that the band gap decreased compared with the independent electron approximation. For 10.3 V/nm, the band gap decreased over time. In this case, the number of electron-hole pairs increases due to tunneling transitions over time, leading to a reduction in the band gap. This change in the band gap is an interesting phenomenon that can be experimentally verified using photoelectron spectroscopy. Taking into account not only the band-gap variation but also changes in the effective mass, we used Equation (1) to evaluate the tunneling-transition rate enhancement factor. Our results indicate that this explanation accounts for 49 and 75% of the enhancement for the two electric-field amplitudes, respectively, but does not fully explain the phenomenon. This suggests that, in addition to static changes in the electronic state, time-dependent polarization oscillations of electron-hole pairs contribute to the tunneling-transition rate enhancement [5].

Fig. 4. Time evolution of the band gap under a steady electric field applied to a system with extremely strong electron-hole interactions ((a) 5.14 V/nm, (b) 10.3 V/nm). Results for TD-qHF (solid blue line) and the IES (solid orange line). Reprinted with permission from Ref. [4]. Copyright 2023 by American Physical Society.

The results of this study can be used to assess the transition rate under a steady electric field but do not directly answer the question, “How fast can light and matter interact?” We attempt to provide an answer on the basis of our findings. Since light has a characteristic oscillation period, it is natural to assume that this timescale sets the fundamental limit for light-matter interactions. However, in the regime of extreme nonlinear optics, the electric-field amplitude becomes a key parameter that determines the interaction timescale through nonlinear effects. Our study has shown that when an electric field on the order of volts/nanometer is applied, electronic oscillations with frequencies corresponding to the material’s band gap can be induced within a few femtoseconds. Thus, our study suggests that even if the photon energy is lower than the band gap, strong optical fields applied to a material can induce light-matter interactions at timescales defined by the material’s band gap.

4. Future prospects

We demonstrated that electron-electron interactions cause variations in the response timescale of electrons to an applied electric field. While the tunneling-transition rate, which played a central role in this study, is in principle an observable quantity, directly measuring it experimentally remains extremely challenging, making it, for now, merely a theoretical construct. To facilitate the experimental measurement of the tunneling-transition rate, we are currently exploring approaches such as introducing another timescale—the oscillation period of an alternating electric field—and investigating how the tunneling-transition rate varies depending on the temporal waveform of the applied field. By comparing theoretically predicted and experimentally measurable physical quantities, we aim to further elucidate the mechanisms of ultrafast electron dynamics and develop methods for controlling these dynamics.

The main theme of this study was the modification of the tunneling-transition rate due to electron-electron interactions. However, experimental materials inherently exhibit such interactions and cannot be artificially removed. This limitation represents a fundamental challenge in assessing the significance of our research. To address this, we propose interpreting our findings from the perspective of transient-property control under applied electric fields and exploring the potential for ultrafast control of anisotropic material properties mediated by many-body effects. For example, when a linearly polarized optical field is applied along a specific direction, the electron-hole distribution may become anisotropic in both the parallel and perpendicular directions with respect to the field. If the material is originally isotropic, this anisotropy in the electron-hole distribution should manifest as an observable change in its physical properties. Since this anisotropy originates from many-body effects, it is expected that we can effectively evaluate many-body phenomena through experimentally measurable quantities. If a technology for ultrafast control of material anisotropy can be established, it may serve as the foundation for a new class of ultrafast optoelectronic devices.

References

[1]	C. Zener, “A Theory of the Electrical Breakdown of Solid Dielectrics,” Proc. R. Soc. London, Ser. A, Vol. 145, No. 855, pp. 523–529, 1934. https://doi.org/10.1098/rspa.1934.0116
[2]	M. Holthaus, “Bloch Oscillations and Zener Breakdown in an Optical Lattice,” J. Opt. B: Quantum Semiclass. Opt., Vol. 2, No. 5, p. 589, 2000. https://doi.org/10.1088/1464-4266/2/5/306
[3]	S. Y. Kruchinin, F. Krausz, and V. S. Yakovlev, “Colloquium: Strong-field Phenomena in Periodic Systems,” Rev. Mod. Phys., Vol. 90, No. 2, p. 021002, 2018. https://doi.org/10.1103/RevModPhys.90.021002
[4]	Y. Shinohara, H. Sanada, and K. Oguri, “Enhancement of Zener Tunneling Rate via Electron-hole Attraction within a Time-dependent Quasi-Hartree-Fock Method,” Phys. Rev. B, Vol. 108, No. 13, p. 134309, 2023. https://doi.org/10.1103/PhysRevB.108.134309
[5]	T. Ikemachi, Y. Shinohara, T. Sato, J. Yumoto, M. Kuwata-Gonokami, and K. L. Ishikawa, “Time-dependent Hartree-Fock Study of Electron-hole Interaction Effects on High-order Harmonic Generation from Periodic Crystals,” Phys. Rev. A, Vol. 98, No. 2, p. 023415, 2018. https://doi.org/10.1103/PhysRevA.98.023415