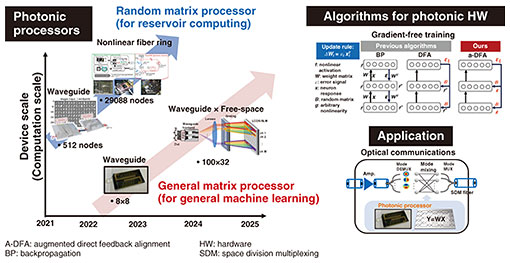
Space and Wavelength Multiplexed Programmable Photonic Processors

1. Introduction

The astonishing advancement in machine learning based on deep neural networks (DNNs) has shown its effectiveness in a wide range of applications such as image generation, machine translation, and physical simulation [1]. This rapid advancement raised critical issues regarding the energy consumption of such computations. For example, large language models require approximately 10²⁵ computations, which consume hundreds of megawatts of energy and emit large amounts of carbon dioxide [2, 3]. These issues have motivated research to achieve more efficient computations on alternative analog hardware using various physical platforms by considering the analogy between the physical laws and computation of the neural network models.

Programmable photonic processors have been intensively studied since they promise massively parallelized computation with low energy consumption for tensor processing in machine learning [4]. The inherent parallelism of light in space, frequency, and time divisions enables parallel and wide-bandwidth processing, which significantly reduces latency and energy consumption compared with electronic processors. A photonic processor would be a promising alternative for machine learning and telecommunications where the bottleneck is the linear processing of its electronic counterparts. In this article, we describe our progress in photonic processors and their application to machine learning and optical communications, as shown in Fig. 1 [5–12].

Fig. 1. Research activity for programmable photonic processors in our research group.

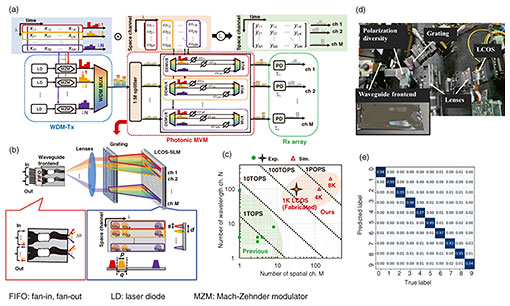
2. Large-scale photonic tensor processor with hybrid waveguide and free-space optics

Photonic matrix-vector multiplication (MVM) based on linear optics is a fundamental component of photonic analog machine learning. A common implementation is wavelength division multiplexing (WDM)-defined tensor processing, as shown in Fig. 2(a). The processor is composed of a WDM-transmitter (Tx), photonic MVM device, and receiver (Rx) array. In this scheme, the N input WDM signals are split into M branches, which are dispersed with a WDM demultiplexer (DMUX) and weighted with variable optical attenuators independently. They are then multiplexed with a WDM multiplexer (MUX) and detected with photodetectors (PDs). The operations per second (OPS) of this configuration can be estimated from the following equation: OPS=2NMB, where N is the number of WDM channels and B is the baud rate of the signal. Thus, the scalability is equal to the M×N value of the photonic MVM device. We developed a scalable photonic MVM device using a hybrid waveguide and free-space optics technology [5, 6]. Figure 2(b) shows a simplified schematic of the architecture of our MVM device. With this device, we can independently control densely multiplexed WDM signals by controlling the wavefront of each beam with a liquid-crystal-on-silicon (LCOS) spatial light modulator (SLM). Figure 2(c) shows the scalability of our MVM device. We constructed an optical benchtop (Fig. 2(d)) supporting M=32 and N=100 as a demonstration, which can be considered to achieve a computation speed of 188 tera OPS (TOPS) by assuming B=30 Gbaud. For the computation benchmark, we executed convolution processing in a convolutional neural network (CNN). We obtained 95.8% accuracy in a handwritten digit recognition task on the Modified National Institute of Standards and Technology (MNIST) dataset (Fig. 2(e)), suggesting successful operation of our device.

Fig. 2. Schematic of (a) WDM-based tensor processing and (b) our photonic MVM device. (c) Reported scalabilities of WDM-based photonic computation. The dashed lines indicate achievable OPS, assuming B=30 Gbaud. (d) Image of fabricated photonic MVM device. (e) Confusion matrix for MNIST task.

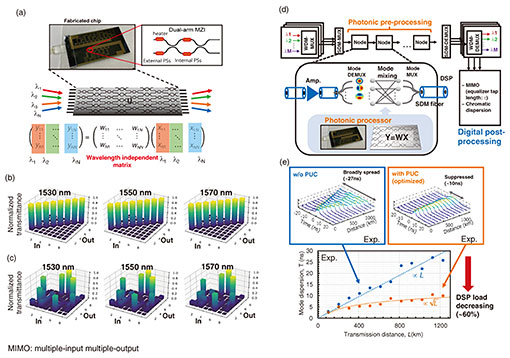
3. WDM-compatible MZI mesh for telecom application

A Mach-Zehnder interferometer (MZI) mesh is another promising candidate for a matrix operation engine [7, 8]. It can execute MVM for each wavelength channel on the basis of spatial parallelism. Thus, multiple MVMs, which correspond to the matrix-matrix multiplication (MMM) used for tensor processing in machine-learning-specific hardware, can be executed at one time by inputting the WDM signal when the weights on the MZI mesh are insensitive to changes in wavelength. We used our silica-based photonic platform technology, called a planar lightwave circuit (PLC) [9], to integrate a wideband MZI mesh [5]. Figure 3(a) shows a photograph of a mesh-type 8×8 integrated photonic processor. Figures 3(b) and (c) show the measured transmitted identity and random matrices for 1530, 1550, and 1570 nm. The results suggest that the photonic processor can compose the same matrices over the examined spectral region. The achievable computation speed is estimated to be >128 TOPS, assuming >10-Gbaud operation with 100 wavelength channels.

A significant use case of the photonic processor in optical communications is as a photonic pre-processor installed in each optical node to reduce the load of the digital signal processor (DSP) [8, 9]. We demonstrated mode-permutation optimization by using an on-chip photonic MZI mesh for long-haul spatial division multiplexed (SDM) transmission (Fig. 3(d)). Our integrated photonic unitary converter (PUC) provided seamless switching capability between weak to strong mode-coupling regimes, which suppresses modal dispersion by controlling the modal mixing state. By optimizing the parameters in the PUC, we achieved 1331-km three-mode transmissions while reducing the equalizer length (Fig. 3(e)).

Fig. 3. (a) Concept of MMM operation using multiple wavelengths. The photo shows the fabricated 8×8 MZI mesh. Measured transmission matrices at 1530, 1550, and 1570 nm when implementing (b) identity matrix and (c) random unitary matrix. (d) Schematic of mode permutation for SDM transmission using the MZI mesh. (e) Required equalizer length as a function of transmission length. By optimizing the MZI mesh, the modal dispersion was suppressed by 60%, reducing the DSP load.

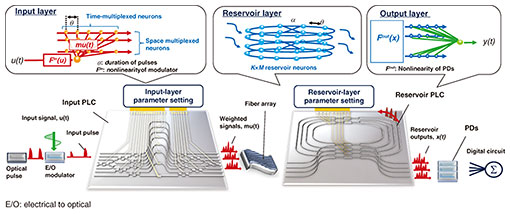
4. Space/wavelength/time multiplexed photonic reservoir computer on chips

On the basis of the above-described MVM functions, we can implement neural network operations beyond simple linear algebra into photonic circuits. We demonstrated an on-chip photonic reservoir computer (RC) integrated with our PLC [10]. In the RC framework, only the output weights are trained while the optical weights are set randomly. Thus, there is no need for any fine tuning of the optical system during training. As the training time is determined by forward propagation in the RC, it can be accelerated using photonics. In spite of the simple training, photonic RCs have performed well in a series of benchmark tasks, such as speech and image recognition.

Figure 4 shows a schematic of our photonic RC. In contrast to previous on-chip implementations of the RC, both the input and reservoir weights are optically encoded in the spatiotemporal domain, which enables scalable integration on a compact chip. Although the nonlinear activation functions are only implemented in the input and output, the complex-valued evolution in coherent systems ensures rich dynamics comparable to that of incoherent nonlinear systems. Our photonic RC supports parallel processing on the basis of WDM, which enables the use of an extremely wide optical bandwidth (>THz) as a computational resource. Experiments with standard benchmarks showed good performance for chaotic time-series forecasting and image classification with extremely fast processing speeds (e.g. 17.1 ns for 28×28 image classification). The photonic RC can execute 21.12 tera multiplication–accumulation OPS (MAC・s^-1) for each wavelength and reach petascale computation speeds on a single photonic chip by using WDM parallelism. Signal processing for optical communications, such as nonlinear equalization, signal format identification, and phase retrieval, have been demonstrated for practical applications using a photonic RC scheme.

Fig. 4. Schematic of our photonic RC. An input-to-reservoir connection (input mask) is generated in the optical domain by using an optical convolutional filter. An array of L optical cavities with N temporal nodes acts as an RC system with N×L virtual nodes, which enables a large-scale implementation on optical chips and ultrafast processing beyond the bandwidth limitation on radio frequency (RF) inputs.

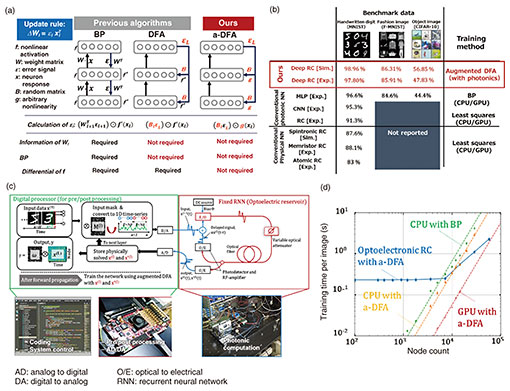
5. Gradient-free training for photonic neural networks

While photonic neural networks mimic analog information processing of the brain, the learning procedure still relies on methods optimized for digital processing because of the difficulty in achieving a photonic implementation of a standard training algorithm such as backpropagation (BP), which otherwise limits the application of photonic processing to the training stage. We previously proposed BP-free photonic deep-learning method [11, 12] that involves using a biologically inspired training algorithm called augmented direct feedback alignment (a-DFA). Figure 5(a) compares the BP, DFA, and our a-DFA algorithms. Our a-DFA algorithm uses fixed random linear transformations of the error signal at the final output layer instead of the backward error signals used with the BP and DFA algorithms. We replace the differential of the physical nonlinear activation ƒ’(a) with an arbitrary nonlinearity g(a). For example, for a standard multilayer perceptron (MLP) network [described as x^(l+1) = ƒ(a^(l)), where a^(l) = W^(l)x^(l) with weight W^(l) and input x^(l) for the lth layer], we can estimate the error for each layer e^(l) as follows: e^(l) = [B^(l) e^(L)] ⨀ g(a^(l)), where B^(l) is a random projection matrix for the lth layer. From e^(l), we can compute the gradient for each W^(l) as δW^(l) = −e^(l)x^(l),T. Thus, we can update the network from the final error e^(L) and alternative random nonlinear projection of the given a^(l), which no longer requires knowledge of the original networks. We can also execute such a random nonlinear projection on a scalable photonic engine. Although we only described a simple MLP model case above, our photonic deep-learning method is scalable to modern networks (e.g. MLP-mixer, ResNet, and Transformer) and photonic-hardware-familiar networks (e.g. spiking neural networks and RCs). As a demonstration, Fig. 5(b) summarizes the test accuracies of each model trained using the a-DFA and BP (baseline) algorithms in a numerical simulation using the MNIST dataset. We also experimentally confirmed the effectiveness of the a-DFA training on our photonic RC shown in Fig. 5(c). The competitive performance of our biologically inspired deep-learning method on the benchmarks (Fig. 5(d)) shows its potential for accelerated computation.

Fig. 5. (a) Comparison of training method of DNNs. (b) Classification accuracy on benchmark tasks. (c) Constructed deep photonic RC. (d) Comparison of training time per image between the photonic processor and central processing unit/graphics processing unit (CPU/GPU).

6. Summary

We reported our progress in scaling up photonic computing platforms. Thanks to the dense parallelization of both space and wavelength divisions, our photonic processor for matrix multiplications can reach computational speeds on sub-petascale OPS. We also described an on-chip integration of a photonic recurrent neural network, called an RC, and a gradient-free machine-learning algorithm for the analog photonic hardware that uses our biologically inspired training method.

References

[1]	Y. LeCun, Y. Bengio, and G. Hinton, “Deep Learning,” Nature, Vol. 521, pp. 436–444, 2015. https://doi.org/10.1038/nature14539
[2]	N. C. Thompson, K. Greenewald, K. Lee, and G. F. Manso, “The Computational Limits of Deep Learning,” arXiv:2007.05558, 2020.
[3]	E. Strubell, A. Ganesh, A. McCallum, “Energy and Policy Considerations for Deep Learning in NLP,” arXiv:1906.02243, 2019.
[4]	B. J. Shastri, A. N. Tait, T. Ferreira de Lima, W. H. P. Pernice, H. Bhaskaran, C. D. Wright, and P. R. Prucnal, “Photonics for Artificial Intelligence and Neuromorphic Computing,” Nat. Photonics, Vol. 15, pp. 102–114, 2021. https://doi.org/10.1038/s41566-020-00754-y
[5]	M. Nakajima, K. Tanaka, K. Inoue, K. Nakajima, and T. Hashimoto, “Densely Parallelized Photonic Tensor Processor on Hybrid Waveguide/Free-Space-Optics,” 2023 International Conference on Photonics in Switching and Computing (PSC), Mantova, Italy, 2023. https://doi.org/10.1109/PSC57974.2023.10297253
[6]	M. Nakajima, K. Ikeda, and T. Hashimoto, “Photonic Convolution Processing with Large-scale Spectral Shaper and Frequency Comb,” The 45th Conference on Lasers and Electro-Optics (CLEO 2025), 4236825, Long Beach, CA, USA, May 2025.
[7]	K. Ikeda, M. Nakajima, S. Kita, A. Shinya, M. Notomi, and T. Hashimoto, “High-fidelity WDM-compatible Photonic Processor for Matrix-matrix Multiplication,” The 44th Conference on Lasers and Electro-Optics (CLEO 2024), JTh2A-87, Charlotte, North Carolina, USA, May 2024.
[8]	M. Nakajima, K. Shibahara, K. Ikeda, A. Kawai, M. Notomi, Y. Miyamoto, and T. Hashimoto, “Programmable Photonic Unitary Processor Enables Parametrized Differentiable Long-haul Spatial Division Multiplexed Transmission,” arXiv:2505.17381, 2025.
[9]	K. Shibahara, K. Ikeda, M. Nakajima, A. Kawai, A. Shinya, M. Notomi, T. Hashimoto, and Y. Miyamoto, “Long-haul Three-mode-multiplexed Transmission Employing On-chip Mode Permutation Technique Based on a Programmable Photonic Unitary Processor,” 2024 IEEE Opto-Electronics and Communications Conference (OECC 2024), 194, Melbourne, Australia, June/July 2024. https://doi.org/10.1109/OECC54135.2024.10975380
[10]	M. Nakajima, K. Tanaka, and T. Hashimoto, “Scalable Reservoir Computing on Coherent Linear Photonic Processor,” Commun. Phys., Vol. 4, 20, 2021. https://doi.org/10.1038/s42005-021-00519-1
[11]	M. Nakajima, K. Inoue, K. Tanaka, Y. Kuniyoshi, T. Hashimoto, and K. Nakajima, “Physical Deep Learning with Biologically Inspired Training Method: Gradient-free Approach for Physical Hardware,” Nat. Commun., Vol. 13, 7847, 2022. https://doi.org/10.1038/s41467-022-35216-2
[12]	M. Nakajima, Y. Zhang, K. Inoue, Y. Kuniyoshi, T. Hashimoto, and K. Nakajima, “Reservoir Direct Feedback Alignment: Deep Learning by Physical Dynamics,” Commun. Phys., Vol. 7, 411, 2024. https://doi.org/10.1038/s42005-024-01895-0