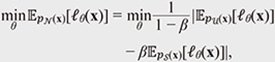1. Introduction
Diffusion models [1] are powerful generative models and have been applied to various fields such as image generation, speech synthesis, and natural language processing. The training of diffusion models can be regarded as the maximization of the evidence lower bound (ELBO), which is the tractable lower bound of the log-likelihood, on the training data [1]. Users collect these training data from sources such as the Internet to generate the content they want then conduct training.
Unfortunately, diffusion models often generate inappropriate, discriminatory, or harmful content that is unwanted by users [2]. For example, they might generate sexual images of real individuals [3]. We refer to such content as sensitive data. The primary cause of this problem is that the training data collected from the Internet inevitably contain such sensitive data. Since the training data are very large, it is difficult to manually remove all sensitive data. When using pre-trained models to generate training data, unintended sensitive data may also be produced. This indicates the difficulty in preparing clean normal data while maintaining the size of the dataset; the training data at hand are not always normal, but mostly unlabeled mixture of both normal and sensitive data. However, it is easy to prepare a small amount of sensitive data that users may not want. Hence, we need to train diffusion models in the positive-unlabeled (PU) setting [4], in which we have access only to unlabeled and sensitive (positive) data but not to normal (negative) data.
We propose PU diffusion models, which prevent the generation of sensitive data for this PU setting. We model an unlabeled data distribution with a mixture of normal and sensitive data distributions. Accordingly, the normal data distribution can be rewritten as a mixture of unlabeled and sensitive data distributions. We thus approximate the ELBO for normal data only using unlabeled and sensitive data. Therefore, even without labeled normal data, we can maximize the ELBO for normal data and minimize it for labeled sensitive data. Note that our method requires only a small amount of labeled sensitive data because such data are less diverse than normal data.
Figure 1 showcases the effect of the PU setting in contrast to the unsupervised setting with only unlabeled data using a handwritten digit dataset called Modified National Institute of Standards and Technology (MNIST). In these examples, even numbers are considered normal data, while odd numbers are considered sensitive data. Our method can maximize the ELBO for normal data (even numbers) and minimize it for sensitive data (odd numbers), using only unlabeled and sensitive data. Therefore, the diffusion model trained with our method generates only normal data (even numbers).
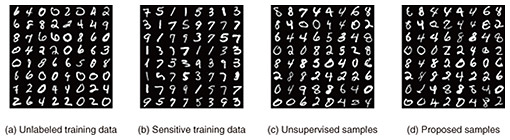
Fig. 1. MNIST examples with the proposed method, where even numbers are considered normal data and odd numbers are considered sensitive data. (a) The unlabeled training data contain 10% sensitive data (odd numbers). (b) The sensitive training data contain only odd numbers. (c) When the diffusion model is trained with the unsupervised method using the unlabeled training data, the generated samples include sensitive data (odd numbers). (d) When the proposed method is applied to the diffusion model, it generates only normal data (even numbers).
Through experiments across real-world datasets and settings, we demonstrated that our method effectively prevents the generation of sensitive images without compromising image quality.
2. Preliminaries
2.1 Problem setting
We first describe our problem setup. Suppose that we are given unlabeled dataset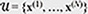 
and labeled sensitive dataset 
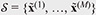for training. Both normal and sensitive data points are included in 
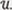Our goal is to train diffusion models so that they generate only normal data using 
.
2.2 Diffusion models
We then review diffusion models [1]. They consist of two processes: diffusion and denoising. The diffusion process gradually adds Gaussian noise to the original data point x0 over T steps, eventually converting it into standard Gaussian noise xT. The denoising process gradually removes the noise from xT using the noise estimator εθ, converting it back to the original data point x0. The noise estimator is trained to minimize the squared error between the estimated noise and true noise for all steps:
where 𝔼[・] is the expectation, xt is the data at time step t, and ε is the true noise added at that step, which follows a standard Gaussian distribution. This squared error corresponds to the negative of the ELBO, which is the tractable lower bound of the log-likelihood [1]. After the training, we can generate data from noise by using the noise estimator.
In standard diffusion model training, all unlabeled data points in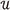 
are assumed normal, and the following objective function is minimized:
However, since the unlabeled data often contain sensitive data, the model trained with the above objective may generate sensitive data.
3. Proposed method
Our proposed method, PU diffusion models, prevents diffusion models from learning sensitive data using . Our method is based on PU learning for training a binary classifier to distinguish between positive and negative data using positive and unlabeled data [4]. We refer to normal data points as negative (−) samples and sensitive data points as positive (+) samples.
To handle 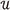that contains sensitive data, we introduce a PU learning framework into the supervised diffusion model. Let 
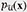represent the unlabeled data distribution, 
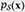the sensitive data distribution, and 
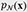the normal data distribution. Datasets are assumed drawn from 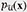and 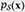, respectively.
We model 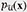with a mixture of 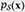and :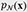
where β ∈ [0,1] is the hyperparameter that represents the ratio of the sensitive data in 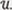Accordingly, 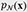can be rewritten as follows:
If we have access to 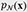, we want to minimize 
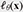for normal data:
and maximize it for sensitive data:
However, we cannot access normal data. On the basis of the PU learning assumption, we approximate training on normal data by using unlabeled and sensitive data:
where we used the absolute value operator according to a previous study [5] because the left-hand side is always positive. We optimize this objective using a stochastic optimization method such as AdamW [6].
4. Experiments
We conducted experiments using Stable Diffusion 1.4 [7] with the following experimental settings. The objective was to ensure that specific individuals (in this case, Brad Pitt) are excluded when generating images of middle-aged men using Stable Diffusion.
The dataset was prepared as follows:
- Unlabeled data: 64 images of middle-aged men and 16 images of Brad Pitt
- Labeled sensitive data: 20 images of Brad Pitt
These images were generated using Stable Diffusion with the prompts “a photo of a middle-aged man” and “a photo of Brad Pitt.” This experimental setup is an extension of that in a previous study [8] to the PU setting.
Using this dataset, we applied the standard fine-tuning (unsupervised) method, the supervised method using supervised diffusion models with which we assume all unlabeled data points to be normal, and the proposed method to Stable Diffusion 1.4.
As an evaluation metric, we use the non-sensitive rate, which represents the ratio of the generated samples classified as normal (non-sensitive) by a pre-trained classifier. It equals one if all generated samples belong to the normal class and zero if they all belong to the sensitive class. We use this metric to evaluate the frequency with which the diffusion model generates sensitive data. For the pre-trained classifier, we use a ResNet-34 [9] fine-tuned on 1000 images each of middle-aged men and Brad Pitt, generated using Stable Diffusion. The accuracy on the test set for the classification task is 99.75%.
The experimental setup is as follows; the batch size is 16, the learning rate is 10−5 for the proposed method and 10−4 for the other methods, the number of epochs is 1000, and β is 0.2 for the proposed method.
The experimental results for generating images of middle-aged men are provided in Fig. 2 and non-sensitive rates are listed in Table 1, where we assume all unlabeled data to be normal and use unlabeled and sensitive data for training with the supervised method. With the unsupervised and supervised methods, attempts to generate images of middle-aged men often resulted in the generation of Brad Pitt. This issue arose due to the presence of Brad Pitt in the unlabeled data. The proposed method successfully suppressed the generation of Brad Pitt.
Fig. 2. Generated samples from fine-tuned stable diffusion models (middle-aged man).
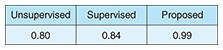
Table 1. Comparison of non-sensitive rates for fine-tuned stable diffusion models.
5. Conclusion
We proposed PU diffusion models, which prevent diffusion models from generating sensitive data by using unlabeled and sensitive data. With the proposed method, we apply PU learning to diffusion models. Thus, even without labeled normal data, we can maximize the ELBO for normal data and minimize it for labeled sensitive data, ensuring the generation of only normal data. We conducted fine-tuning of Stable Diffusion 1.4 and confirmed that the proposed method can improve the non-sensitive rate of generated samples without compromising image quality. In the future, we will focus on analyzing hyperparameters and further improving generation quality.
References
| [1] |
J. Ho, A. Jain, and P. Abbeel, “Denoising Diffusion Probabilistic Models,” Advances in Neural Information Processing Systems 33, pp. 6840–6851, 2020. |
| [2] |
M. Brack, P. Schramowski, F. Friedrich, D. Hintersdorf, and K. Kersting, “The Stable Artist: Steering Semantics in Diffusion Latent Space,” arXiv preprint arXiv:2212.06013, 2022. |
| [3] |
Y. Mirsky and W. Lee, “The Creation and Detection of Deepfakes: A Survey,” ACM Computing Surveys (CSUR), Vol. 54, No. 1, 2021. |
| [4] |
R. Kiryo, G. Niu, M. C. du Plessis, and M. Sugiyama, “Positive-unlabeled Learning with Non-negative Risk Estimator,” Advances in Neural Information Processing Systems 30, pp. 1674–1684, 2017. |
| [5] |
Z. Hammoudeh and D. Lowd, “Learning from Positive and Unlabeled Data with Arbitrary Positive Shift,” Advances in Neural Information Processing Systems 33, pp. 13088–13099, 2020. |
| [6] |
I. Loshchilov and F. Hutter, “Decoupled Weight Decay Regularization,” arXiv preprint arXiv:1711.05101, 2017. |
| [7] |
R. Rombach, A. Blattmann, D. Lorenz, P. Esser, and B. Ommer, “High-resolution Image Synthesis with Latent Diffusion Models,” Proc. of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, June 2022. |
| [8] |
A. Heng and H. Soh, “Selective Amnesia: A Continual Learning Approach to Forgetting in Deep Generative Models,” Advances in Neural Information Processing Systems 36, pp. 17170–17194, 2023. |
| [9] |
K. He, X. Zhang, S. Ren, and J. Sun, “Deep Residual Learning for Image Recognition,” Proc. of the 2026 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016. |
 |
- Hiroshi Takahashi
- Research Scientist, Learning and Intelligent Systems Research Group, Innovative Communication Laboratory, Communication Science Laboratories, NTT, Inc.
He received a B.E. in computer science from Tokyo Institute of Technology in 2013, M.E. in computational intelligence and systems science in 2015, and Ph.D. in informatics from Kyoto University in 2023. He joined NTT in 2015 and has been investigating machine learning. His research interests include generative models such as diffusion models, large language models, and anomaly detection.
|
