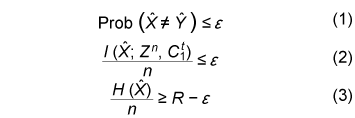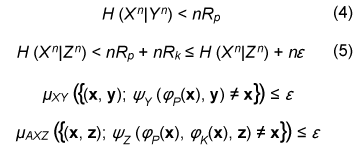Some Results on Secret Key Agreement Using Correlated Sources

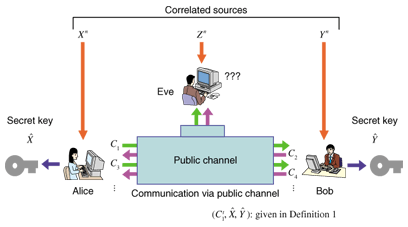
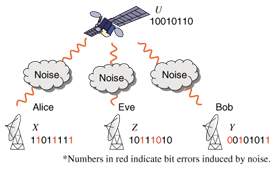
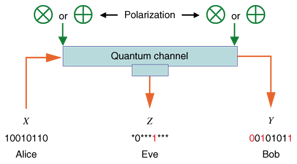
1. Introduction

When two users want to exchange messages securely, they can use encryption as long as both of them know the secret key. We consider the situation in which legitimate users Alice and Bob and an eavesdropper Eve each has access to a correlated source. To transmit messages securely, Alice and Bob must agree on a secret key. Secret key agreement, which is introduced in [1], is the procedure for agreeing on a secret key by exchanging messages over a public channel (see Fig. 1). The colored arrows indicate information disclosure.The above situation can be achieved by introducing the scenario presented in [1] (see Fig. 2). In this scenario, a satellite broadcasts messages U that are unknown to Alice, Bob, and Eve. They have antennas that enable them to receive the messages. Inevitably, there is noise between the satellite and each antenna: these noises are independent. Thus, Alice, Bob, and Eve have access to correlated sources (X, Y, Z), which are the respective outputs of mutually independent channels with the input corresponding to the broadcast message. It should be noted that there is another scenario related to quantum cryptography [2]. By using a quantum channel, Alice and Bob can share a correlated sequence, while Eve can also acquire a sequence that is correlated with that of Alice and Bob by wiretapping the quantum channel (see Fig. 3).

Fig. 1. Secret key agreement from correlated sources.

Fig. 2. Satellite scenario.

Fig. 3. Quantum channel scenario.

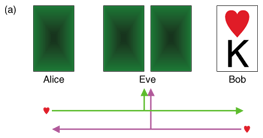
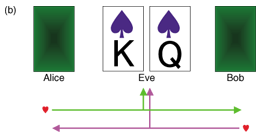
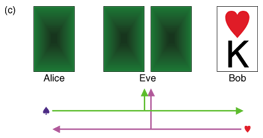
To understand how secret key agreement is performed, we present an example of correlated sources that was introduced in [3]. Assume that there are only four cards {♠K, ♠Q, ♥K, ♥Q}. A trusted dealer shuffles these four cards and deals them to Alice, Bob, and Eve. Alice and Bob execute the following key agreement protocol at each deal.

1. Alice and Bob each reveals the suit of their own card.
2. If they know that they both have the same suit, they agree on the key ‘0’ if Alice has the king, which implies that Bob has the queen and the key ‘1’ if Alice has the queen, which implies that Bob has the king.
3. If they know that they have different suits, they give up trying to agree on a key in this round and discard this deal.

In Fig. 4(a), let us assume that we are Bob. Bob has ♥K and knows that Alice also has ♥. Therefore, we can conclude that Alice must have ♥Q and we can agree on the key ‘1’. In Fig. 4(b), let us assume that we are Eve. Eve knows that both Alice and Bob have ♥, but she cannot know that who has ♥K or who has ♥Q, even when she has the other two cards. This implies that Alice and Bob can agree on 1 bit for a secret key. In Fig. 4(c), let us again assume that we are Bob. Bob has ♥K and knows that Alice has ♠, but not whether it is ♠K or ♠Q. In this case, Alice and Bob give up trying to achieve key agreement for this deal because neither of them can determine the partner’s card.

The following are important goals in the study of secret key agreement.

1. Design a secret key agreement protocol that is practical.
2. Estimate the secret key capacity, which corresponds to the optimal efficiency of the secret key generation.
3. Estimate the supremum of the secret key capacity over a class of correlated sources.

It should be noted that the secret key capacity estimation is necessary in order to design a secure system.

This paper deals with the following topics. In section 2, we review the formal definition of the secret key agreement protocol and the secret key capacity introduced by Maurer [1]. Section 3 describes a scheme for secret key agreement using correlated sources. We obtain the result that there is a pair of sparse matrices, known as low-density parity check (LDPC) matrices, that yields secret key agreement using correlated sources. Algorithms using sparse matrices are known to have practically efficient decoding algorithms such as the Belief Propagation (BP) algorithm [4] and Linear Codes Linear Program (LCLP) algorithm [5]. By using LDPC matrices with one of the practical decoding algorithms, our construction is computationally efficient. However, it should be noted that information reconciliation is performed only approximately. In section 4, we introduce the advantage distillation capacity, which provides a naive information theoretical expression for the secret key capacity introduced in [6], which is the least upper bound of the key generation rate of the secret key agreement. In section 5, we investigate the capacity for secret key agreement under a sampling attack. We analyze the supremum of the normalized secret key capacity defined as the supremum of the secret key capacity divided by the description length of the alphabet*, where the supremum is taken over some class of correlated sources. In particular, we consider symmetric sources and derive inequalities that show the scaling of the secret key capacity.

Fig. 4. Example of secret key agreement.

2. Definition of secret key agreement protocol and secret key capacity

The secret key capacity, which is the least upper bound of the key generation rate in the secret key agreement, was first introduced by Maurer [1]. Before defining it, we define the protocol that describes the procedure of Alice and Bob. Let X, Y, and Z be three sources available to Alice Bob, and Eve, respectively. Let Xⁿ ≡(X₁, X₂, …, X_n), Yⁿ≡ (Y₁, Y₂, …, Y_n), and Zⁿ≡ (Z₁, Z₂, …, Z_n). The entropy of a random variable V, conditional entropy of random variable V with given random variable W, and mutual information between random variables V and W are denoted by H (V), H (V | W), and I (V ; W), respectively. Let C_i^j ≡ (C_i, …, C_j) for i ≤ j; here, the symbol C_i^j is ignored when i > j.

Definition 1: A protocol (C₁^t, ˆX, ˆY ) for (X, Y, Z) with t steps is composed of the following procedure:

1. If i is odd, Alice sends C_i over an insecure but authenticated channel, where C_i is computed from Xⁿ and C₁^i-1. If i is even, Bob sends C_i over an insecure but authenticated channel, where C_i is computed from Yⁿ and C₁^i-1.
2. Alice and Bob repeat the transmission of C_i while 1 ≤ i ≤ t.
3. Finally, Alice computes ˆX from Xⁿ and C₁^t, and Bob computes ˆY from Yⁿ and C₁^t.

Formally, random variables (Xⁿ, Yⁿ, Zⁿ, C₁^t,ˆX,ˆY ) satisfy the following conditions:

where U ↔ V ↔ W denotes the Markov chain satisfying pUVW (u, v, w) = pUV (u, v) pW|V (w|v) for all (u, v, w).

Definition 2: We call the protocol (C₁^t, ˆX, ˆY ) given in Definition 1 a secret key agreement protocol for (X, Y, Z) with rate R ≥ 0 if (C₁^t, ˆX, ˆY ) satisfies

for all ε > 0 and all sufficiently large n. The secret key capacity S(X;Y||Z) of the sources is defined as the least upper bound of such R for all possible key agreement protocols.

Condition (1) means that we can perform a secret key agreement with an arbitrarily small error probability. Condition (2) means that the secret key and Eve’s information are mutually independent and she cannot obtain any information about the secret key. It should be noted that we consider (unconditional) information theoretical security [7], which is different from computational security [8] such as public key cryptography.

An open problem has been to give the explicit information theoretical expression for the secret key capacity for general correlated sources. The upper and lower bounds of S(X;Y||Z) are given in [1], [9].

3. Construction of secret key agreement protocol using LDPC matrices

In this section, we assume that I(X; Y) > I(X; Z) and that feedback is not allowed in the secret key agreement; that is, t=1. Let μXYZ be the joint distribution of (Xⁿ, Yⁿ, Zⁿ). We assume that codes for correlated sources (Xⁿ, Yⁿ, Zⁿ) satisfy

for any ε > 0 and all sufficiently large n, where (x, y, z) is the output of (Xⁿ, Yⁿ, Zⁿ). Such codes can be constructed by using the LDPC matrices proposed in [10]. Let X be a finite field and x∈Xⁿ be represented by a column vector. Let P and K be 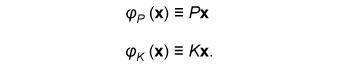nR_P × n and nR_K × n LDPC matrices, respectively. We next define φ _P and φ_K by

We define φ_Y and φ_Z by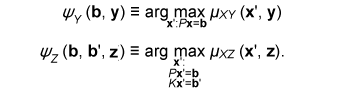

A secret key agreement protocol is constructed below.

1. Alice transmits C₁ ≡ φ_P(Xⁿ) to Bob.
2. Alice generates a secret key by ˆX ≡ φ_K (Xⁿ). Bob generates a secret key by ˆY ≡ φ_K (ψ_y(C₁, Yⁿ)).
   

The error probability of the secret key agreement is expressed by
Prob (ˆX ≠ ˆY )

We have the following theorem. The proof is given in [10].

Theorem 1: Assume that μXYZ satisfies Eqs. (4) and (5). There are LDPC matrices K and P such that the above secret key agreement protocol (C₁, ˆX, ˆY ) satisfies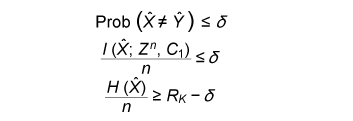

for all δ> 0 and all sufficiently large n.

4. Secret key capacity and advantage distillation capacity

In this section, we introduce the advantage distillation capacity. According to [11], there are three phases in a secret key agreement.

Advantage distillation: When the correlation between X and Y is weaker than or equal to those between X and Z and between Y and Z, i.e.,

the aim of this protocol (C₁^t , ˆX, ˆY ) is to provide Alice and Bob with an advantage over Eve; that is,

An example of this technique is presented in [1].

Information reconciliation: This technique allows Alice and Bob to obtain an identical random sequence from the output of (X, Y) by using this protocol while minimizing the amount of information leaked to Eve.

Privacy amplification: This is a technique for obtaining a secret key sequence from the above identical random sequence.

In section 3, the construction of a combined information reconciliation and privacy amplification protocol was provided by assuming that I(X; Y) > I(X; Z). In the following, we focus on an advantage distillation protocol and investigate the difference [I(ˆX; ˆY ) – I(ˆX; Zⁿ, C₁^t )]/n of a protocol (C₁^t , ˆX, ˆY ). Let us define the advantage distillation capacity.

Definition 3: We call the protocol (C₁^t , ˆX, ˆY ) given in Definition 1 an advantage distillation protocol for (X, Y, Z) with rate R ≥ 0 if the difference [I(ˆX; ˆY ) – I(ˆX; Zⁿ, C₁^t )]/n is equal to R; that is,

The advantage distillation capacity D(X;Y||Z) of the sources is defined as the least upper bound of such R for all possible advantage distillation protocols; that is,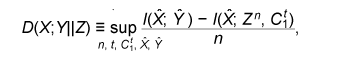

where the supremum is taken over n, t, and random variables (C₁^t , ˆX, ˆY ) generated by a protocol with step t.

It should be noted that conditions (1) and (2) are not required for the advantage distillation protocol and that condition (3) is replaced by (6). These points are the differences from the definition of secret key capacity.

We obtain the following theorem in relation to secret key capacity and advantage distillation capacity. Proof of this theorem is given in [6].

Theorem 2: Let X, Y, and Z be three sources available to Alice, Bob, and Eve, respectively. Then,

This theorem implies that we can construct an optimum secret key agreement protocol by using an advantage distillation protocol achieving advantage distillation capacity and a combined information reconciliation and privacy amplification protocol with rate [I(ˆX; ˆY ) – I(ˆX; Zⁿ, C₁^t )]/n for distilled sources (ˆX, ˆY, (Zⁿ, C₁^t )). The function D(X; Y||Z) provides information theoretical expressions of secret key capacity. It should be noted here that this expression is not a single-letter characterization and that the alphabets of random variables and the number of steps of a protocol are not bounded in the supremum. The single-letter characterization of the secret key capacity is presented in [9] for some particular source examples.

5. Secret key capacity for optimally correlated sources under a sampling attack

In the following, we investigate the satellite scenario introduced in [1], where three sources (X, Y, Z) have a common latent random variable U, and X, Y, and Z are the respective outputs of mutually independent channels for input U. Let U be the finite alphabet of U. Then, the joint probability distribution μXYZ of (X, Y, Z) is given by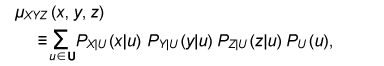

where PX|U, PY|U, and PZ|U are the conditional probability distributions of the respective channels and pU is a probability distribution corresponding to U. Then, we have

for any random variable (X, Y, Z) with a common latent variable U, where the left inequality is given in [1]. Inequality (7) implies that the secret key capacity of the satellite scenario is zero if Eve has access to the latent variable.

Next, we consider the situation where Eve obtains m samples z^m∈Z^m. Then, the joint probability corresponding to (X, Y, Z^m) is expressed by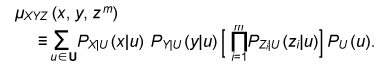

Furthermore, we assume that pZ_i|U does not depend on i and we denote it by pZ|U. Then, from Eq. (7) and the result presented in [12], there exists α ≥ 0 such that

where |•| denotes the cardinality of a set. This inequality implies that it becomes easier for Eve to predict the latent parameter U by a sampling attack and that the secret key capacity decreases exponentially as the number of Eve’s samples increases when α > 0.

In the following, we assume that the statistical properties of the correlated source can be adjusted for a given number of Eve’s sources in order to optimize the secret key capacity. It should be noted here that it may be possible to increase the secret key capacity by increasing the size of the alphabet. In fact, the upper bound of Eq. (8) can be relaxed by increasing the alphabet size. On the other hand, it is natural to consider the cost of receiving one random symbol. For this reason, we define normalized secret key capacity by S(X; Y||Z^m)/log₂|A|, where A is an alphabet of random variables X, Y, Z₁ …, Z^m. We investigate the supremum of the normalized secret key capacity under a sampling attack defined in the following.

Definition 4: For a given number m of Eve’s samples, we define the supremum of normalized secret key capacity ¯S (S|m) of the set of sources S by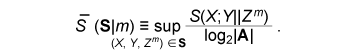

We introduce the following scenario for the definition of symmetric sources. A trusted server broadcasts message U, which is unknown to any users. Each terminal receives the message via mutually independent noisy channels. Thus, the correlated sources (A₁, …, A_k) are the respective outputs of mutually independent noisy channels with input U. We assume that channels have identical characteristics. We call a correlated source (A₁, …, A_k) symmetric if there are U, pU, and pA|U such that

where U is the alphabet of U. The following theorem states that the supremum of the normalized secret key capacity for the class of all symmetric sources is close to O(1/m).

Theorem 3: The supremum of the normalized secret key capacity for symmetric sources S_sym under a sampling attack is bounded by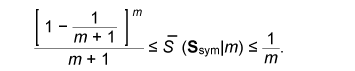

The proof is given in [3].

6. Conclusion

We studied the secret key agreement introduced in [1], which is a procedure for agreeing on a secret key by using correlated source outputs and exchanging messages over a public channel. First, we presented a practical secret key agreement protocol that uses LDPC matrices. Next, we analyzed the advantage distillation capacity, which provides a naïve information theoretical expression of the secret key capacity. Finally, we analyzed the secret key agreement under a sampling attack. We observed that the secret key capacity decreases exponentially as the number of Eve’s samples increases when the distribution of a channel is fixed. Then, we analyzed the supremum of normalized secret key capacity defined as the supremum of the secret key capacity for all possible sources. It is O(1/m) for symmetric sources.

References

[1]	U. M. Maurer, “Secret key agreement by public discussion from common information,” IEEE Trans. Inform. Theory, Vol. IT-39, No. 3, pp. 733–742, 1993.
[2]	C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” Proc. of IEEE Int. Conf. on Comp. Sys. and Signal Proc. of Bangalore, India, pp. 175–179, 1984.
[3]	J. Muramatsu, K. Yoshimura, K. Arai, and P. Davis “Secret key capacity for optimally correlated sources under sampling attack,” IEEE Trans. Inform. Theory, Vol. IT-52, No. 11, pp. 5140–5141, 2006.
[4]	F. R. Kschischang, B. J. Frey, and H. A. Loeliger, “Factor graphs and the sum-product algorithm,” IEEE Trans. Inform. Theory, Vol. IT-47, No. 2, pp. 498?519, 2001.
[5]	J. Feldman, M. J. Wainwright, and D. R. Karger, “Using linear programming to decode binary linear codes,” IEEE Trans. Inform. Theory, Vol. IT-51, No. 3, pp. 954–972, 2005.
[6]	J. Muramatsu, K. Yoshimura, and P. Davis, “Secret key capacity and advantage distillation capacity,” IEICE Transactions on Fundamentals, Vol. E89-A, No. 10, pp. 2589?2596, Oct. 2006.
[7]	C. E. Shannon, “Communication theory of secret system,” Bell System Technical Journal, Vol. 28, pp. 656?715, 1949.
[8]	W. Diffie and M. Hellman, “New directions in cryptography,” IEEE Trans. Inform. Theory, Vol. IT-22, No. 6, pp. 644–654, 1976.
[9]	R. Ahlswede and I. Csisz'ar, “Common randomness in information theory and cryptography––Part I: Secret sharing,” IEEE Trans. Inform. Theory, Vol. IT-39, No. 4, pp. 1121–1132, 1993.
[10]	J. Muramatsu, “Secret key agreement from correlated source outputs using low density parity check matrices,” IEICE Trans. Fundamentals, Vol. E89-A, No. 7, pp. 2036?2046, 2006.
[11]	C. H. Bennett, G. Brassard, C. Crepeau, and U. M. Maurer, “Generalized privacy amplification,” IEEE Trans. Inform. Theory, Vol. IT-41, No. 6, Part 2, pp. 1915–1923, 1995.
[12]	F. Kanaya and T. S. Han, “The asymptotics of posterior entropy and error probability for Bayesian estimation,” IEEE Trans. Inform. Theory, Vol. IT-41, No. 6, pp. 1988–1992, 1995.

↑ TOP