You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Regular Articles: New Paradigm toward Realizing Quantum Computer

Vol. 9, No. 7, pp. 25–28, July 2011. https://doi.org/10.53829/ntr201107ra2

Reducing the Resources in Measurement-only Quantum Computation

Yasuhiro Takahashi^†

Abstract

This article describes a recent result concerning the construction of a small set of projective measurements required for implementing universal quantum computation, that is, for implementing an arbitrary unitary operation. Projective measurements are used as the main resources for implementing an arbitrary unitary operation in the measurement-only quantum computation model in contrast to conventional models. Resource minimization is important not only for realizing a quantum computer based on the measurement-only quantum computation model, but also for understanding the computational power of projective measurements.

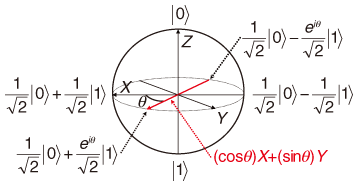
†	NTT Communication Science Laboratories Atsugi-shi, 243-0198 Japan

1. Introduction

Quantum computers are expected to enable high-speed computing and many researchers have made numerous attempts to realize them. However, a practical quantum computer has not yet been made. Most of the attempts are based on the standard model of quantum computation, which is called the quantum circuit model or gate-based quantum computation [1], [2]. The main resources for universal quantum computation, that is, for implementing an arbitrary unitary operation, are unitary gates that perform one-qubit and two-qubit unitary operations. A computation proceeds by applying unitary gates to an input state to transform it into an appropriate output one. Projective measurements of the output state give us the final output of the computation, which is classical information.

In 2003, on the basis of an idea described by Gottesman and Chuang [3], Nielsen proposed a model of quantum computation [4] strikingly different from the standard model. This model is called teleportation-based or measurement-only quantum computation. The main resources required for universality are only projective measurements. A computation proceeds by performing projective measurements on an input state to transform it into an appropriate output one. Projective measurements on the output state give us the final output of the computation. This model has recently attracted attention since it allows us to make completely new attempts to realize quantum computers. An important problem is to minimize the resources required for universality. From the practical standpoint, solutions to this problem will contribute to the performance of unitary operations on a quantum computer since it will be able to use only a limited amount of resources. On the theoretical side, they will contribute to our understanding of the computational power of projective measurements.

Let us consider the problem of minimizing the resources required for universality in measurement-only quantum computation. There have been many studies in this direction [5]–[8]. The best known result is that a set consisting of one two-qubit projective measurement and infinitely many kinds of one-qubit projective measurements with one ancillary qubit is sufficient for universal quantum computation [8]. Since it is impossible to decrease the number of two-qubit projective measurements and the number of ancillary qubits, we shall focus on one-qubit projective measurements. Thus, our problem is restated as the problem of constructing a small set of one-qubit projective measurements such that the set with one two-qubit projective measurement and one ancillary qubit is sufficient for universal quantum computation.

The state of a qubit corresponds to a point on the unit three-dimensional sphere (Fig. 1) [1] and a one-qubit projective measurement corresponds to an axis, which is a line through the origin of the sphere. There are two points of intersection between an axis and the sphere. A one-qubit projective measurement proba-bilistically projects a one-qubit state into one of the two states corresponding to the two intersection points on the sphere. The best known result requires the set consisting of one-qubit projective measurements corresponding to all the axes of the sphere’s X-Y plane and the Z axis [8]. Until recently, it was not known whether a smaller set of one-qubit projective measurements could be constructed for universal quantum computation.

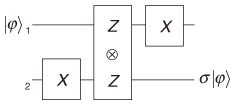
Fig. 1. Unit three-dimensional sphere representing one-qubit states.

In this article, I describe my recent result that this can be done [9]. Specifically, I show that the set consisting of one-qubit projective measurements corresponding to all the axes of the sphere’s X-Y plane (with one two-qubit projective measurement and one ancillary qubit) is sufficient for universal quantum computation. In other words, I show that the one-qubit projective measurement corresponding to the Z axis can be removed from the best known set. A key finding is that the one-qubit projective measurement corresponding to the Y axis can often be used in place of the one-qubit projective measurements corresponding to the X and Z axes. In particular, a key ingredient of my procedure for implementing an arbitrary one-qubit unitary operation is a simplified version of quantum teleportation (called state transfer) based on the one-qubit projective measurement corresponding to the Y axis.

2. Measurement-only quantum computation

2.1 Quantum states and projective measurements

As described above, the state of a qubit corresponds to a point on the unit three-dimensional sphere (Fig. 1). The two points of intersection of the Z axis and the sphere are represented by |0 and |1. The other points on the sphere correspond to superposition states of |0 and |1. For example, the two points of intersection of the X axis and the sphere are

|0 + |1 and |0 − |1. Moreover, the two points of intersection of the Y axis and the sphere are |0 + |1 and |0 − |1. In general, a one-qubit state is represented as α|0 + β|1, where α and β are complex numbers such that |α|² + |β|²=1.

A one-qubit projective measurement corresponds to an axis L, which is a line through the sphere’s origin. It probabilistically projects a one-qubit state into one of the two states corresponding to the two points of intersection of L and the sphere. The probability depends on the state being measured. The measurement gives us the classical outcome (1 or -1) representing which of the two states the original state is projected into by the measurement. We call such a measurement an L-measurement. For example, the Z-measurement of a qubit in state α|0 + β|1 projects the state into |0 with probability |α|² and into |1 with probability |β|². In general, an axis of the sphere’s X-Y plane is represented by (cosθ)X+(sinθ)Y for some real number θ∈[0,2π). It corresponds to the one-qubit projective measurement that probabilistically projects a one-qubit state into one of the two states

|0 + |1 and |0 - |1.

2.2 Measurement-based quantum circuits

A computational procedure in measurement-only quantum computation can be represented by a measurement-based quantum circuit (very similar to the standard quantum circuit [2]). It consists of wires and measurement gates that correspond to qubits and projective measurements, respectively. In a circuit diagram, a wire is represented by a horizontal line and a measurement gate is represented by the axis symbol corresponding to the projective measurement on the wires on which it is performed. Information flows through the circuit from left to right.

As an example, consider the measurement-based quantum circuit depicted in Fig. 2. It represents the following procedure, where the initial state of qubit 1 is |φ and that of qubit 2 is an arbitrary one-qubit state.

(1) Perform the X-measurement on qubit 2.

(2) Perform the ZZ-measurement on qubits 1 and 2.

(3) Perform the X-measurement on qubit 1.

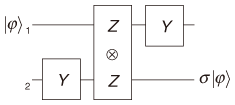
I do not give details of the ZZ-measurement here, but in general it generates a two-qubit state that cannot be represented as a product form (called entangled state).

Fig. 2. Measurement-based quantum circuit proposed for state transfer [6].

The procedure outputs the state σ |φ on qubit 2 for some unitary operation σ, which is in a special class of unitary operations called Pauli operations. An important point is that σ is determined by the classical outcomes of the projective measurements in the procedure, and the inverse of s can be performed by the Y-measurements (and one two-qubit projective measurement and one ancillary qubit). Thus, σ can be easily removed and thus ignored. That is, the procedure transfers an arbitrary one-qubit state from qubit 1 to qubit 2 (up to Pauli operations) and thus is called state transfer [6]. It can be regarded as a simplified version of quantum teleportation.

As shown in [6], state transfer is a key ingredient of a procedure for implementing an arbitrary one-qubit unitary operation. More precisely, a procedure for implementing such an operation (up to Pauli operations) can be obtained by replacing the projective measurements in the state transfer with ones that depend on the desired operation. For example, a procedure for implementing a Hadamard operation H can be obtained by replacing the first measurement with the Z-measurement and the second measurement with the ZX-measurement, where H is the one-qubit unitary operation that maps |0 and |1 to

|0 + |1 and |0 − |1, respectively.

3. Universal set of projective measurements

I will show that the set consisting of the one-qubit projective measurement corresponding to the axis (cosθ)X+(sinθ)Y for any θ∈[0,2π) (with one two-qubit projective measurement and one ancillary qubit) is sufficient for universal quantum computation. To do this, I will show that an arbitrary unitary operation can be implemented using only the above projective measurements. Since an arbitrary unitary operation can be implemented by combining one-qubit unitary operations with a two-qubit unitary operation [1], it suffices to show how to implement these operations.

3.1 New state transfer

A key ingredient of my procedure for implementing an arbitrary one-qubit unitary operation is a new state transfer based on the Y-measurements. Consider the following procedure (Fig. 3), where the initial state of qubit 1 is |φ and that of qubit 2 is an arbitrary one-qubit state.

(1) Perform the Y-measurement on qubit 2.

(2) Perform the ZZ-measurement on qubits 1 and 2.

(3) Perform the Y-measurement on qubit 1.

Fig. 3. State transfer based on Y-measurements.

The procedure can be shown to be a state transfer, which transfers the input state from qubit 1 to qubit 2. It is obtained by replacing the X-measurements in the previous state transfer with the Y-measurements. That is, this is an example of the case where the Y-measurements can be used in place of the X-measurements.

3.2 Implementations of one-qubit and two-qubit unitary operations

I will deal with one-qubit unitary operations first. I can show that, by replacing the ZZ-measurement in the new state transfer with the ZX-measurement, the resulting procedure is the one for implementing H. An important point is that it uses only Y-measurements, though the previous procedure for implementing H uses the X- and Z-measurements as described above. This can be considered an example of the case where the Y-measurements can be used in place of the X- and Z-measurements. That is, the new state transfer provides an H implementation procedure that requires only a small set of one-qubit projective measurements. By generalizing the method for transforming the new state transfer into an H implementation procedure, I can obtain a procedure for implementing an arbitrary one-qubit unitary operation (up to Pauli operations). Moreover, I can show that it requires only the one-qubit projective measurement corresponding to the axis (cosθ)X+(sinθ)Y for any θ∈[0,2π).

As a two-qubit unitary operation, it suffices to deal with the controlled- Z operation Λ Z that maps |0|0, |0|1, |1|0, and |1|1 to |0|0, |0|1, |1|0, and −|1|1, respectively. The remaining problem is to obtain a procedure for implementing Λ Z (up to Pauli operations) using only the one-qubit projective measurement corresponding to the axis (cosθ)X+(sinθ)Y for any θ∈[0,2π). Though it is difficult to implement Λ Z directly, I can show that there is a two-qubit unitary operation similar to Λ Z such that combining it with one-qubit unitary operations implements an arbitrary unitary operation and that it can be implemented by using only Y-measurements. Thus, the set consisting of the one-qubit projective measurement corresponding to the axis (cosθ)X+(sinθ)Y for any θ∈[0,2π) is sufficient for universal quantum computation.

4. Conclusions and future work

I examined the problem of minimizing the resources required for universality in measurement-only quantum computation and described a small set of projective measurements sufficient for universal quantum computation. A key ingredient of my procedures is state transfer based on the Y-measurements. It would be interesting to consider approximate universality in measurement-only quantum computation [10] because a small approximately universal set of projective measurements is particularly important in practice. Moreover, it would be interesting to investigate the resources required for other important problems, such as graph state preparation [9].

References

[1]	M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, 2000.
[2]	Y. Takahashi, “Quantum Arithmetic Circuits: a Survey,” IEICE Trans. Fundamentals, Vol. E92-A, No. 5, pp. 1276–1283, 2009.
[3]	D. Gottesman and I. L. Chuang, “Demonstrating the Viability of Universal Quantum Computation Using Teleportation and Single-qubit Operations,” Nature, Vol. 402, pp. 390–393, 1999.
[4]	M. A. Nielsen, “Quantum Computation by Measurement and Quantum Memory,” Phys. Lett. A, Vol. 308, No. 2-3, pp. 96–100, 2003.
[5]	D. W. Leung, “Quantum Computation by Measurements,” International Journal of Quantum Information, Vol. 2, No. 1, pp. 33–43, 2004.
[6]	S. Perdrix, “State Transfer Instead of Teleportation in Measurement-based Quantum Computation,” International Journal of Quantum Information, Vol. 3, No. 1, pp. 219–223, 2005.
[7]	A. M. Childs, D. W. Leung, and M. A. Nielsen, “Unified Derivations of Measurement-based Schemes for Quantum Computation,” Phys. Rev. A, Vol. 71, No. 3, 032318, 2005.
[8]	P. Jorrand and S. Perdrix, “Unifying Quantum Computation with Projective Measurements Only and One-way Quantum Computation,” Proc. of SPIE Quantum Informatics 2004, Vol. 5833, pp. 44–51, 2005.
[9]	Y. Takahashi, “Simple Sets of Measurements for Universal Quantum Computation and Graph State Preparation,” International Journal of Quantum Information, Vol. 8, No. 6, pp. 1001–1012, 2010.
[10]	S. Perdrix, “Towards Minimal Resources of Measurement-based Quantum Computation,” New Journal of Physics, Vol. 9, No. 6, 206, 2007.

Yasuhiro Takahashi: Scientist, Computing Theory Research Group, Innovative Communication Laboratory, NTT Communication Science Laboratories.
He received the B.S. and M.S. degrees in mathematics from Tohoku University, Miyagi, and the Ph.D. degree in engineering from the University of Electro-Communications, Tokyo, in 1998, 2000, and 2008, respectively. He joined NTT Communication Science Laboratories in 2000 and has been engaged in research on the design and optimization of quantum circuits including measurement-based ones. His research interests include quantum computing, computational complexity theory, and cryptography. He is a member of the Information Processing Society of Japan and the Institute of Electronics, Information and Communication Engineers.

↑ TOP