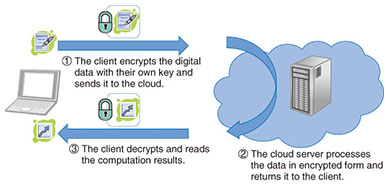
Fully Homomorphic Encryption over the Integers: From Theory to Practice

1. Fully homomorphic encryption

In recent years, we have been entrusting more and more of our electronic data to the cloud, including e-mail, internal company documents, and personal information. Protecting the privacy and confidentiality of that data is a major challenge for today’s security researchers and practitioners. A 2013 study by the Cloud Security Alliance revealed a worrying increase in the number of major data breach incidents in which cloud data was leaked as a result of negligence, malware, or insider attacks [1]. Cryptographers have proposed several possible approaches to addressing the problem of cloud security without compromising on functionality. One of the most promising approaches is fully homomorphic encryption, which has garnered a lot of attention in recent years.

Encrypting data before sending it to the cloud is a simple way of guaranteeing confidentiality. Parties who do not own the decryption key, including malicious hackers and the cloud server operators themselves, cannot learn anything about the data that was encrypted. Therefore, that data remains safe even in the case of a breach. However, if one uses traditional encryption, it also becomes impossible for the cloud operators to carry out any kind of processing of that data (even searching it, for example), as they would have to decrypt it first. This defeats the purpose of most applications of cloud computing. Fortunately, fully homomorphic encryption eliminates that limitation. Data encrypted with fully homomorphic encryption enjoys essentially the same security guarantees as with traditional encryption, but it becomes possible to carry out arbitrary computations on it without decrypting it first. The result of those computations remains in encrypted form, and can thus only be recovered by the owner of the decryption key. That unique property makes it possible to build a wide range of highly secure cloud services.

2. Potential applications

The most direct application of fully homomorphic encryption is probably outsourced computation (Fig. 1). Consider a scenario in which a client has some sensitive data to process but lacks the required expertise or sufficient computational power; as a result, they want to commission a cloud service to carry out the processing, but without revealing this sensitive data in plaintext form. Fully homomorphic encryption offers a simple solution to that problem; the client simply sends the data to the cloud server in encrypted form, and the server processes the data without decrypting it using the property of fully homomorphic encryption (this computation on encrypted data is called homomorphic evaluation of the corresponding function). Finally, the client receives the encrypted output from the server and decrypts it with his key, obtaining the result of the processing without having revealed any information about the sensitive data. For example, cloud services already exist that perform backtesting of stock market trading strategies, but professional traders are unlikely to rely on them for fear of revealing highly valuable strategies. With fully homomorphic encryption, however, it is possible to provide a backtesting cloud service to traders while ensuring that their valuable techniques will remain safe from prying eyes (even those of the cloud operators themselves!). Similarly, one can imagine cloud services that provide DNA (deoxyribonucleic acid) analysis for medical institutions and law enforcement authorities while maintaining the confidentiality of DNA samples, or services that perform mechanical structural analysis for the aerospace or construction industries without asking clients to compromise the secrecy of their designs.

Fig. 1. Outsourced computation based on fully homomorphic encryption.

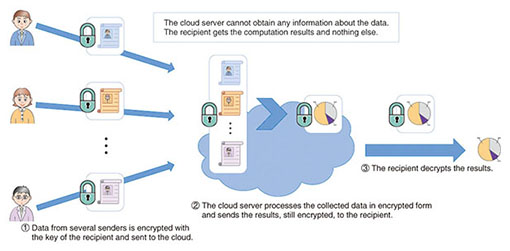
Another application of fully homomorphic encryption is anonymous data processing (Fig. 2). This kind of scenario involves multiple users sending some sensitive data to a cloud server, where it is aggregated, stripped of identifying information, and analyzed, typically to extract some statistical information, which is then delivered to the final recipient. The security requirement is that the cloud server must learn nothing about the content of users’ data, and the recipient must obtain only the anonymized results of the statistical analysis, and in particular, no information on individual users. This can also be achieved using fully homomorphic encryption; the users first use a fully homomorphic encryption scheme to encrypt their own data under the recipient’s public key and send it to the cloud server. The data collected on the server is then processed in encrypted form using homomorphic evaluation. The result of this processing is the anonymized statistical information, also in encrypted form. That output is then sent to the recipient, who finally decrypts it. Possible applications of such a protocol include secure electronic voting, where individual voters encrypt their ballots with the public key of the organizer of the vote and then send them to a tallying server. The server uses homomorphic evaluation to carry out validity checks on encrypted ballots and to compute the encrypted tally, which is then sent to the organizer, who finally decrypts that aggregate result without learning individual votes. Secure auctions and statistical analysis of medical data are other possible uses.

Fig. 2. Anonymous data processing with fully homomorphic encryption.

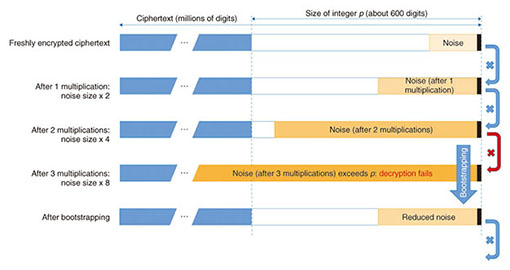
There are also examples of cloud services for which fully homomorphic encryption is not well suited. One is encrypted search on a database. The reason for this is that the server cannot obtain any information on the content of the search query, so homomorphic evaluation of the search operation requires processing the entire database from beginning to end, rather than just a small portion of it, making the whole operation very computationally costly. A secure web search service based on fully homomorphic encryption, for example, would be prohibitively impractical. Similarly, spam filtering of encrypted e-mail and other services that require the cloud server itself to obtain the result of processing encrypted information cannot be implemented using homomorphic encryption. In the case of spam filtering, for example, processing e-mail using homomorphic evaluation would yield a list of messages detected as spam in encrypted form, making it impossible for the server itself to delete them without asking the client to decrypt that list first, a rather inconvenient process.

Despite such limitations, though, fully homomorphic encryption is undoubtedly a very promising technology for cloud security—if only it can be made efficient enough for practical applications. At the NTT Secure Platform Laboratories, we are hard at work trying to achieve this goal.

3. Fully homomorphic encryption over the integers

The concept of fully homomorphic encryption itself was proposed in the late 1970s, but constructing an actual fully homomorphic encryption scheme remained an open problem for a long time; in fact, many cryptographers believed that it was impossible. In 2009, however, Craig Gentry of Stanford University disproved this widely held belief by describing the first fully homomorphic encryption scheme. The following year, he also proposed, together with van Dijk, Halevi, and Vaikuntanathan, a conceptually simpler construction of fully homomorphic encryption, based entirely on integer arithmetic. These results were major theoretical breakthroughs, but the proposed schemes were both extremely inefficient; thus, the problem of fully homomorphic encryption, while solved in theory, remained open as far as practical implementations were concerned.

Here is a succinct, somewhat simplified description of the original fully homomorphic encryption scheme over the integers of van Dijk et al. An important observation is that to obtain a secure fully homomorphic scheme that supports the encryption of arbitrary messages and the homomorphic evaluation of arbitrary functions on ciphertexts, it is in fact sufficient to construct a scheme to encrypt single-bit messages (either 0 or 1) and evaluate an arbitrary number of XOR and AND logic gates on encryptions of those bits. Indeed, data of any length can be represented as a bit string, and arbitrary functions on such a bit string can be represented as Boolean circuits (consisting of XOR (exclusive OR) and AND gates) on the corresponding bits. By encrypting each bit of the bit string independently and applying the homomorphic evaluation of the XOR and AND gates of the Boolean circuits, we obtain the required fully homomorphic functionality.

In fully homomorphic encryption over the integers, the secret key is a relatively large odd integer p (of about 600 digits, say). Given several multiples q_ip of p, it is easy to recover p by computing the greatest common divisor (GCD). However, recovering p from many approximate multiples of the form q_ip + e_i (where e_i is a relatively small 20- to 30-digit noise value) is believed to be a hard problem. In fact, if q_i is a large enough random integer (a few million digits), the approximate multiple q_ip + e_i is indistinguishable from a random integer of the same size in the view of an attacker who does not know p. As a result, one can encrypt a one-bit message m (0 or 1) by adding to it a large, random multiple q p of p (of a few million digits) as well as some even random noise 2r (of 20 to 30 digits). To an attacker who does not know the secret key p, the resulting ciphertext c = q p + 2r + m is then indistinguishable from a random integer of the same size, as discussed above, regardless of whether m is 0 or 1; hence, attackers cannot learn anything about m from the ciphertext c. On the contrary, the legitimate owner of the secret key p can decrypt the ciphertext c by computing the Euclidean division by p and checking the parity of the remainder 2r + m: it is even if m is 0 and odd if m is 1. Thus, we have described a secure (secret-key) encryption scheme.

Moreover, this encryption scheme supports the homomorphic evaluation of XOR and AND gates. Indeed, consider two single-bit messages m₁ and m₂ and corresponding ciphertexts c₁ and c₂. We claim that the sum c₁ + c₂ is an encryption of m₁ XOR m₂. Indeed, c₁ + c₂ = (q₁ + q₂)p + 2(r₁ + r₂) + (m₁ + m₂), and its remainder in the Euclidean division by p is 2(r₁ + r₂) + (m₁ + m₂). If m₁ = m₂, this is an even number, and hence, c₁ + c₂ decrypts to 0. Similarly, if m₁ ≠ m₂, this is an odd number, and c₁ + c₂ decrypts to 1, as required. We can check in much the same way that the product c₁ c₂ = (q₁q₂p + 2q₁r₂ + q₁m₂ + 2q₂r₁ + q₂r₁)p + 2(2r₁r₂ + r₁m₂ + r₂m₁) + m₁m₂ is a valid encryption of m₁ AND m₂.

Unfortunately, the scheme described above is not quite a fully homomorphic encryption scheme yet; it only satisfies the weaker property of being ‘somewhat homomorphic’. The problem is that whenever a homomorphic XOR and especially AND operation is carried out, that noise value within the ciphertext grows (its size roughly doubles with each AND gate). If too many such homomorphic operations are carried out, at some point the noise value becomes larger than p, at which point it becomes impossible to ensure correct decryption anymore (Fig. 3). Therefore, the scheme we just described does not support the homomorphic evaluation of arbitrary functions, but only of those functions which, when represented as a Boolean circuit, consist of only a limited number of successive levels of AND gates (hence the name somewhat homomorphic encryption). To overcome this problem and enable the homomorphic evaluation of arbitrary functions, it is necessary to devise a procedure to reduce the noise within a ciphertext to some extent. One of the key insights of Gentry’s work is a technique called bootstrapping for exactly that purpose. Applying that technique after each AND gate makes it possible to evaluate arbitrary Boolean circuits, and hence, to obtain proper fully homomorphic encryption.

Fig. 3. Bootstrapping for fully homomorphic encryption.

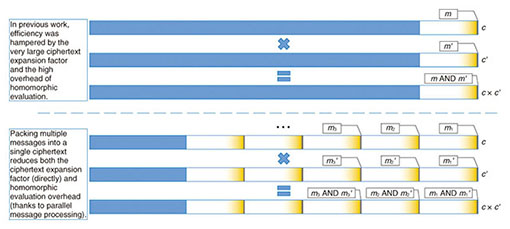
However, the resulting scheme is very inefficient. Even if we consider the somewhat homomorphic scheme, we see that a ciphertext of several million digits is needed to encrypt a single bit; in other words, ciphertexts are millions of times larger than the corresponding plaintexts, and homomorphic operations corresponding to simple XOR and AND gates involve arithmetic on huge integers, requiring both a large amount of memory and lengthy computations. Using bootstrapping to turn the scheme into a fully homomorphic one further reduces the efficiency by a considerable extent. Consequently, something has to be done to approach practical levels of efficiency.

4. Contributions of NTT

Obtaining more practical constructions of fully homomorphic encryption over the integers is one of our research topics at the NTT Secure Platform Laboratories. We face three main challenges that hold back the performance of fully homomorphic encryption over the integers. The first one is ciphertext expansion; as described above, ciphertexts consist of millions of digits for every single message bit. The second one is the overhead of homomorphic evaluation; evaluating an operation as simple as a bitwise AND requires carrying out exact arithmetic on huge integers, which is slow. This problem is further compounded by bootstrapping, which makes each homomorphic operation considerably costlier. The third bottleneck is the size of the public key and of public parameters. So far, we have described a secret key encryption scheme, but many applications such as anonymous data processing require public key encryption. The conversion from secret key to public key for a fully homomorphic scheme can be done in a relatively straightforward manner (it is sufficient to publish a large number of encryptions of 0), but this results in a prohibitively large public key. Moreover, the bootstrapping method requires publishing very large public parameters for homomorphic evaluation, even for secret key schemes.

Until 2012, we mainly tackled the first and third of those problems, and by introducing novel techniques to compress public keys and ciphertexts, as well as a nonlinear optimization of the encryption algorithm, we were able to obtain major efficiency improvements. Public keys and parameters, in particular, went from a size so large that they would barely fit in an entire datacenter, as in the original construction by van Dijk et al., down to only a few megabytes. This increased the speed considerably, as less data had to be processed for homomorphic evaluation, enabling us to obtain a proof of concept implementation executable in reasonable time on an ordinary computer [2].

In 2013, we proposed yet another fully homomorphic encryption scheme over the integers offering dramatic improvements to both ciphertext expansion and homomorphic evaluation overhead at the same time [3]. The key idea was to pack multiple message bits m₁, …, m_n into a single ciphertext in such a way that all of these bits could be processed in parallel during homomorphic evaluation (Fig. 4). To do so, we use several odd numbers p₁, …, p_n as the secret key, and we encrypt the multi-bit message (m₁, …, m_n) as an integer c obtained as a multiple of the product p₁…p_n plus some noise chosen in such a way that the remainder of the Euclidean division of c by p_i is of the form 2r_i + m_i. The Chinese remainder theorem ensures that we can compute such a c, and that the sum and product of two of these ciphertexts respectively encrypt the bitwise XOR and AND of the corresponding multi-bit messages. Putting these many message bits together in a single ciphertext and processing them homomorphically in parallel yield the expected efficiency improvements in terms of ciphertext expansion and homomorphic evaluation complexity. More recently, we proposed a further major improvement by adapting to fully homomorphic encryption over the integers a technique, originally conceived for a different type of schemes, to avoid the use of the expensive bootstrapping method when evaluating arbitrary functions homomorphically [4]. With that technique, homomorphic AND operations only increase the size of ciphertext noise by a small fixed amount instead of doubling it every time. As a result, with a suitable choice of parameters, it becomes possible to evaluate any given Boolean circuit homomorphically and still ensure that the noise size does not exceed the limit of correct decryption, making bootstrapping unnecessary. The new results from 2013 alone enabled us to improve the speed of fully homomorphic encryption of integers by about two orders of magnitude, and to obtain the world’s fastest homomorphic evaluation of the AES (Advanced Encryption Standard) block cipher in about 20 seconds per block on a standard personal computer with no compromise on security. This level of performance already makes homomorphic processing of small amounts of data practical and enables us to envision more ambitious applications in the near future.

Fig. 4. Batch ciphertexts in fully homomorphic encryption.

5. Further work

Going forward, we intend to maintain our status as one of the world’s top research groups investigating fully homomorphic encryption and to continue to innovate with the goal of achieving still more practical levels of efficiency. Since ciphertext compression techniques and other optimizations that were developed for earlier variants of fully homomorphic encryption over the integers cannot be used with our current best scheme, further efficiency improvements are now mainly hampered by memory requirements. Our first objective is to overcome that problem, so as to make the homomorphic processing of larger amounts of data practical. We will also move forward with research on cryptographic multilinear maps, another cutting-edge cryptographic technique with very important applications, the most prominent of which is certainly general program obfuscation. Multilinear maps share a number of structural similarities with fully homomorphic encryption; this has allowed us to propose a new way of constructing them, as well as the first ever implementation of a multilinear map-based protocol.

References

Mehdi Tibouchi Researcher, Okamoto Research Laboratory, NTT Secure Platform Laboratories. He is an alumnus of École normale supérieure in Paris, France and received a Ph.D. in computer science from the University of Paris VII and the University of Luxembourg in 2011. He joined the NTT Secure Platform Laboratories thereafter. His research interests include the design and analysis of public-key cryptographic schemes, with a particular view towards new feature-rich primitives. He is a member of the International Association for Cryptologic Research (IACR) and the European Association for Theoretical Computer Science (EATCS).