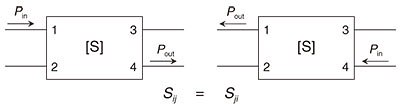
Control of Light with Exceptional Points in Coupled Photonic Crystal Lasers

1. Constraints of optical control in on-chip optical devices

Optical communication is currently at the stage where it is possible to transmit data at speeds on the order of 10 Tbit/s through an optical fiber. It may seem that light can be controlled freely; however, there are limits to the varieties of optical control that are possible in on-chip optical circuits, and there are still problems to be solved for many of the practical applications of these circuits.

The difficulty of optical control arises from the fact that photons have no mass or charge. In other words, it is not possible to control the movements of photons based on conservative forces such as gravity or electromagnetism arising from the energy potential. Therefore, in the range that we normally see, light mainly manifests as electromagnetic (EM) waves. From the Maxwell equation describing the behavior of light, we can derive the property called Lorentz reciprocity (Fig. 1). In systems that are stationary in time and exhibit a linear response to EM waves, this means that scattering matrices showing their EM input-output relationship will have a symmetrical form. In other words, the system’s optical path has exactly the same transmittance (or mode conversion rate) in one direction as that in the opposite direction, and there is no anisotropy. In photonics, therefore, it is not even straightforward to create transistors and diodes (optical isolators), which are common in electronics.

Fig. 1. Lorentz reciprocity for propagating modes. [S] = [S_ij]: the scattering matrix, which relates the input EM waves to the output EM waves, in terms of their amplitudes and phases; i, j: channel indices. In the case of single-channel input power P_i,in at the ith channel, the output power P_j,out at the jth channel is P_j,out = |S_ij|² P_i,in.

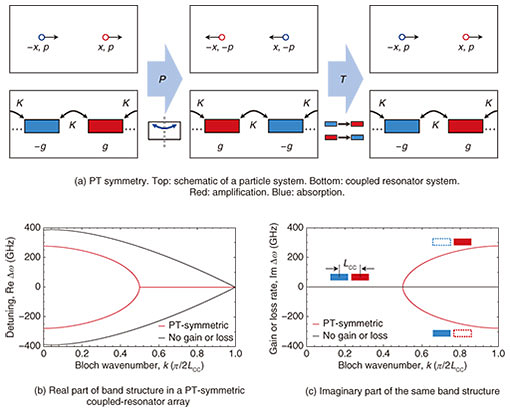
Currently, purely on-chip photonic components, for which technologies have been well established, include waveguides, lasers, intensity and phase modulators, detectors, and interference switches. These components can generally achieve most basic functions such as the generation and detection of coherent light, the control of intensity and phase (modulation), and the switching of optical paths. As long as they are in static operations, they will not significantly violate the abovementioned Lorentz reciprocity. To perform optical control beyond these constraints, the use of other well-known phenomena such as magneto-optic effects and nonlinear optical effects can be considered. However, particularly in microphotonics and nanophotonics, such effects are generally restricted due to the small device sizes and low-intensity input light available. Moreover, there are severe requirements of integration and processing techniques for heterogeneous materials. As a result, efforts to develop devices of this sort are still at the research stage.

In contrast, the field of parity-time (PT)-symmetric optics or exceptional point optics has been rapidly developing, partly because it is based on the prospect of achieving new optical functions by making use of existing technologies.

2. Novel optical phenomena based on PT symmetry (exceptional points)

The concept of PT symmetry was first proposed in 1998 by Carl Bender of Washington University (Missouri, USA) and Stefan Boettcher, who is currently at Emory University (Georgia, USA) [1]. This work was originally aimed at expanding the theoretical framework of quantum mechanics.

The P in PT symmetry represents space inversion, which is the operation of reversing coordinates around a certain origin in the physical system under consideration. Thus, this operation changes an object’s coordinate (position operator) from x to −x and its momentum (momentum operator) from p to −p (Fig. 2(a)).

The T in PT represents time inversion, which is the operation of reversing the direction in which time flows. Thus, it also inverts the sign of an object’s momentum. In addition, for systems interacting with the external environment (reservoir), an increase in the number of particles (signed rate +g) changes to a decrease (−g), and vice versa. In PT symmetry, when these two operations are performed simultaneously, the system behaves in the same way as before the operation. In other words, it is a symmetry that represents invariance in the energy operator (Hamiltonian).

In standard quantum mechanics, closed systems are primarily handled using Hermitian Hamiltonian matrices and the Schrödinger equation. Meanwhile, if we introduce an increase or decrease in the number of particles because of the external environment (non-Hermitian term), then imaginary components arise in energy eigenvalues. In other words, this leads to the inconsistent result in quantum theory, where the energy is not an observable quantity. However, under PT symmetry, this sort of local change in the number of particles can be balanced in the entire system, so the energy eigenvalues can be maintained as observable real quantities.

It is not easy to verify this concept experimentally in quantum systems that rely on the precise manipulation of small numbers of particles. However, the observation in 2008 that an analogy to PT symmetry is possible in optical systems based on classical electromagnetism [2] resulted in an explosion of research on PT-symmetric optics. This is because it was originally recognized in optics studies that gain by stimulated emission and loss in absorption media are natural effects. Furthermore, we can approximate the behavior of light propagating in a material with a thickness on the order of one wavelength (paraxial beam) using the Schrödinger equation. Thus, we can argue that EM waves can also exhibit properties analogous to PT symmetry, which was originally considered in the context of the quantum mechanical wavefunction.

As a result of this groundbreaking work, it was recognized that a PT-symmetric optical system can be implemented as a periodic optical system consisting of amplifying (gain) and absorbing (loss) media with balanced rates (±g) such that the system’s complex refractive index distribution corresponds to n(r) = n^*(−r); that is, the real and imaginary parts of the refractive index are respectively given by even and odd functions with respect to a certain origin. Potential examples of such systems include coupled resonators, coupled waveguides, modulating waveguides with vapor-deposited metal on part of a single waveguide, and fiber ring resonator systems. It has been shown that these systems exhibit a number of novel phenomena originating from the exceptional point (PT phase transition point) as described below.

Examples are shown in Fig. 2(b) and (c) of bulk band structures^*1 for the real and imaginary parts of the eigenfrequency detuning Δω of a PT-symmetric coupled-resonator system (taking the identical resonant frequency of each resonator as the reference frequency, i.e., Δω = 0). Here, the system’s positive imaginary part Im(Δω) > 0 is regarded as a net gain, and Im(Δω) < 0 means a net loss of the eigenstates for each Bloch wavenumber, k, in the unit of π/(2L_CC), where L_CC is the spatial interval between the cavities. As shown in the lower part of Fig. 2(a), this system has two resonators as periodic units (unit cells). In the absence of gain and loss, the real bands are in the form of halved cosine curves (black lines in Fig. 2(b)), and the imaginary band is zero for all possible k (black lines overlapped in Fig. 2(c)).

Fig. 2. PT symmetry and exceptional points.

In contrast, in the band structure of the PT-symmetric system with gain and loss (red lines in Fig. 2(b)), the upper and lower real bands merge at a certain point inside the first Brillouin zone to form a flat region. In the imaginary band structure (red lines, Fig. 2(c)), a new branch is generated from the wavenumber corresponding to the merge point in Fig. 2(b), and it extends to the edge of the band, k = π/(2L_CC). This merge point is called an exceptional point^*2 in complex function theory.

What happens at an exceptional point? In the two states before the real bands merge, light of equal intensity is distributed to both resonators in the unit cell, but in the two states after merging, the light is localized to either the cavity with the amplifying medium or that with the absorption medium. The imaginary band shows the net gains and losses of the state, and in the state before branching occurs, the light spreads evenly to both resonators, indicating that the overall gains and losses cancel each other out.

In the state after branching, on the other hand, light is biased toward one resonator, so there is either a gain or a loss depending on which side the light becomes localized. In other words, a discontinuous qualitative change from an extensive stable state to an unstable localized state occurs at the exceptional point. In the parlance of physics, this is called a phase transition. Therefore, this point is also called the PT phase transition point. However, it is known that this phase transition and its accompanying phenomena can occur without the gains and losses being perfectly balanced.

Various phenomena occur before and after the phase transition [3]. These can be broadly categorized as two types. The first type consists of directional responses resulting from the breaking of spatial inversion symmetry by gains and losses—for example, unidirectional reflectionless resonances—and double refraction in a single direction. In fact, although it is known that Lorentz reciprocity cannot be destroyed in a standard linear PT-symmetric optical system, it has been proved that if the system is combined with nonlinearity in the laser oscillation, it can achieve the optical isolation at weak input intensities [4, 5].

The second type consists of a phenomenon in which the net gain and loss caused by the phase transition are related. A typical example is single-mode lasing. In addition, lasing caused by an increase in loss of the partial system, accompanied by the phase transition, has also been observed (loss-induced lasing).

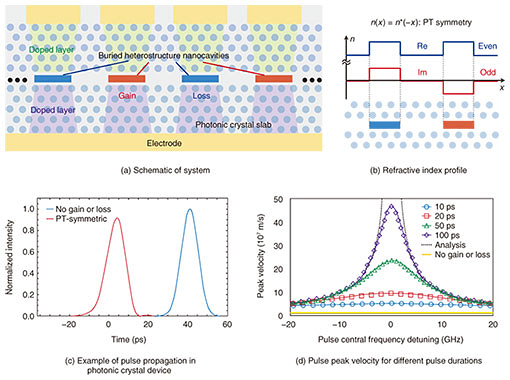
3. Control of light group velocity by an exceptional point using a coupled photonic crystal laser array

To introduce these sorts of optical responses and mode control methods into nanophotonics, we proposed a PT-symmetric coupled-resonator optical waveguide based on arrays of buried-heterostructure photonic crystal lasers, and we conducted a theoretical analysis of the system [6] (Fig. 3(a), (b)). NTT has developed a fabrication technique for a nanolaser that oscillates with the world’s smallest threshold current [7] and has been researching a large-scale Si (silicon) photonic crystal coupled-resonator optical waveguide [8]. By combining these technologies, we hope to achieve devices with new functions like those described above. In particular, we expect it will be necessary to increase the scale of the entire device (the number of cycles of gain and loss media) to control the device’s transmission and reflection well and to increase its achievable output power. However, there are few platforms that support both the scalability and fine control of the amplification and absorption. We will therefore explore the possibility of performing optical control with the merits of scale, based on the use of ultra-miniature lasers with gain and loss tuning by current injection or optical pumping.

As an example, we focused on controlling the group velocity in this coupled-resonator optical waveguide. Group velocity is a measure of the propagation speed of optical communication pulses. It is defined as the gradient of the real band (dΔω/dk) in Fig. 2(c) and diverges to infinity at the frequency corresponding to the exceptional point. In this study, we carried out an analysis using the tight-binding approximation^*3 and the Schrödinger equation to show that despite the group velocity divergence at the exceptional point, the group velocity dispersion, which quantifies the pulse broadening, converges at a finite value there. This suggests that optical pulses may propagate without collapsing even under the extreme condition with a high group velocity.

Next, we conducted a numerical experiment where optical pulses were excited in a PT-symmetric coupled-resonator optical waveguide and propagated through 100 resonators. Here, their central frequencies were close to the exceptional point, that is, Δω = 0. We used the same parameters assumed for the photonic crystal device discussed above. An example of pulse propagation in this experiment is shown in Fig. 3(c). The horizontal axis here is the time from when the center of the excitation pulse passes through the starting point until the signal is detected after passing through 100 resonators. This figure shows the results for a 10-ps pulse. The pulse peak propagates about ten times faster in a PT-symmetric system than in the system without any gain or loss introduced. However, to obtain such a response, we must selectively excite a pulse with a single direction of travel (excitation wavenumber selectivity).

The pulse peak propagation speed increases as the temporal pulse duration increases. This is because a longer temporal width results in a narrower spectral width, which is less susceptible to slow group velocity components and higher order dispersion. The dependence of the peak velocity on the pulse central frequency is shown in Fig. 3(d) for several different pulse durations. The data suggest that a pulse with a temporal width of about 100 ps can in principle accelerate beyond the speed of light in the vacuum. Here, it is reckoned that this acceleration of pulses originating from increases and reductions in intensity does not conflict with the theory of relativity.

Fig. 3. Photonic crystal PT-symmetric coupled-resonator optical waveguide.

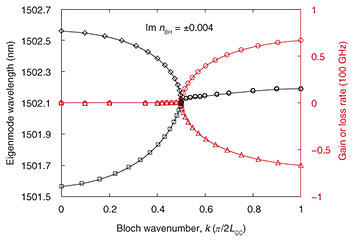
Finally, we calculated the band structure by conducting an EM wave simulation assuming a realistic three-dimensional photonic crystal slab structure and embedding medium. The results are shown in Fig. 4. With suitable gain and loss, the bands exhibit an exceptional point where the principal eigenfrequency detuning component changes from real (black symbols) to imaginary (red symbols) values (respectively represented in the figure as the wavelength and net gain or loss rates). In this case, the signed gain and loss components of the media are about ±300 cm⁻¹, which are realistic for semiconductor optical devices. A closer look at the data indicates that the wavelengths of the two band curves (black lines) do not perfectly coincide near the exceptional point, and the maximum possible group velocity is about nine times as high as that of a system without any gain or loss introduced. This is thought to be due to radiation loss perpendicular to the slab surface, which implies that it is important to design devices with strong optical confinement.

Fig. 4. Band structure of photonic crystal PT-symmetric coupled-resonator optical waveguide.

4. Future prospects

In this article, we described the background of the area of research focused on controlling light by using exceptional points based on PT-symmetric optics. In addition, we theoretically showed the drastic changes in the group velocity in the PT-symmetric photonic crystal laser arrays. We are currently carrying out an experimental demonstration of PT phase transition in a photonic crystal system with two nanolasers and studying advanced theoretical topics including control of photonic topology in coupled laser systems. We are also pursuing a way of implementing large-scale PT-symmetric systems, which we hope to demonstrate in the future.

References

[1]	C. M. Bender and S. Boettcher, “Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry,” Phys. Rev. Lett., Vol. 80, No. 24, pp. 5243–5246, 1998.
[2]	K. G. Makris, R. El-Ganainy, D. N. Christodoulides, and Z. H. Musslimani, “Beam Dynamics in PT Symmetric Optical Lattices,” Phys. Rev. Lett., Vol. 100, No. 10, 103904, 2008.
[3]	L. Feng, R. El-Ganainy, and L. Ge, “Non-Hermitian Photonics Based on Parity-time Symmetry,” Nat. Photon., Vol. 11, No. 12, pp. 752–762, 2017.
[4]	B. Peng, S. K. Özdemir, F. Lei, F. Monifi, M. Gianfreda, G. L. Long, S. Fan, F. Nori, C. M. Bender, and L. Yang, “Parity-time-symmetric Whispering-gallery Microcavities,” Nat. Phys., Vol. 10, No. 5, pp. 394–398, 2014.
[5]	L. Chang, X. Jiang, S. Hua, C. Yang, J. Wen, L. Jiang, G. Li, G. Wang, and M. Xiao, “Parity-time Symmetry and Variable Optical Isolation in Active-passive-coupled Microresonators,” Nat. Photon., Vol. 8, No. 7, pp. 524–529, 2014.
[6]	K. Takata and M. Notomi, “PT-symmetric Coupled-resonator Waveguide Based on Buried Heterostructure Nanocavities,” Phys. Rev. Applied, Vol. 7, No. 5, 054023, 2017.
[7]	T. Kakitsuka and S. Matsuo, “Current-injection Photonic-crystal Laser,” NTT Technical Review, Vol. 10, No. 12, 2012. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201212fa10.html
[8]	E. Kuramochi, T. Tanabe, and M. Notomi, “Silicon-based Large-scale Photonic Crystal Nanocavity Arrays for Slow-light Applications,” NTT Technical Review, Vol. 8, No. 2, 2010. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201002sf5.html